Unit Vector
A unit vector is a vector of unit
length
. Any non-zero vector can be normalized into a unit vector by a division of a vector by its norm, that is
![]() .
.
Note that unit vector is not equal to one vector
![]() , it is the magnitude of the vector is one, not the elements.
, it is the magnitude of the vector is one, not the elements.
Example:
Suppose we have vector
![]()
The norm of the vector is
![]()
Converting it to unit vector becomes
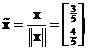
Now the norm of the unit vector is
![]()
The interactive program below will help you to convert your vector input into a unit vector of any positive dimension. The program will also show you the norm of input vector, norm of unit vector (which is always 1) and sum of the unit vector.
Properties
Some important properties of unit vector are
-
The inner product of a unit vector to itself is one
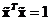 .
.
-
Two unit vectors
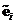 and
and
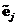 are perpendicular to each other (orthogonal) if and only if
are perpendicular to each other (orthogonal) if and only if
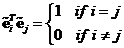 .
.
-
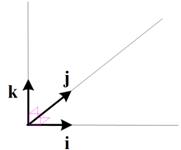
In an Euclidean space, the standard unit vectors that orthogonal to each other has name:
-
unit vector of the first dimension is
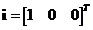
-
unit vector of the second dimension is
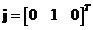
-
unit vector of the third dimension is
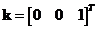
-
unit vector of the first dimension is
-
The dot products of the standard unit vector:
- Dot product of the same standard unit vector is one
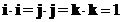
- Dot product of the perpendicular standard unit vector is zero
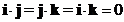
- Dot product of the same standard unit vector is one
-
The cross product of the standard unit vectors:
- Cross product of the same standard unit vector is zero
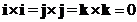
- Cross product of the perpendicular standard unit vector form a cycle
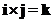 ;
;
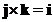 ;
;
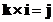 ;
;
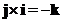 ;
;
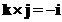 ;
;
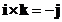
- Cross product of the same standard unit vector is zero
See also
:
dot product
,
cross product
,
vector norm
,
basis vector
<
Next
|
Previous
|
Index
>
Rate this tutorial or give your comments about this tutorial
