Orthogonal Vector
Two vectors are perpendicular (or orthogonal) to each other if and only if their inner product is zero
. Vectors that perpendicular to each other are also called
orthogonal vectors
.
When the two vectors that perpendicular to each other also have unit length (i.e. their norm is one), then these vectors are called orthonormal vectors .
The interactive program below will help you to determine whether your input vectors are orthogonal or not. When you click random example button, the program will give you a lot of examples of both orthogonal vectors and not orthogonal vectors.
Properties
Some important properties of orthogonal & orthonormal vector are
-
Two unit vectors
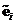and
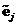are perpendicular to each other (orthogonal) if and only if
.
-
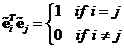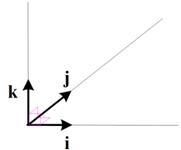
In 3-dimensional Euclidean space, there are 3 standard unit vectors that orthogonal to each other with special name
,
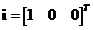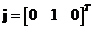and
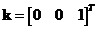. Figure below show the 3 standard orthogonal unit vectors.
-
The dot products of the standard orthogonal unit vector:
-
Dot product of the same standard unit vector is one
-
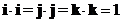
Dot product of the orthogonal standard unit vector is zero
-
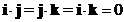
Dot product of the same standard unit vector is one
-
The cross product of the standard unit vectors:
-
Cross product of the same standard unit vector is zero
-
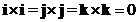
Cross product of the orthogonal standard unit vector form a cycle
;
;
;
;
;
;
-
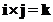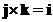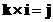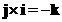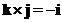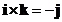Cross product of the same standard unit vector is zero
See also
:
dot product
,
cross product
,
vector norm
Rate this tutorial or give your comments about this tutorial