Statistical Independent
In this section of the tutorial, you will learn the diference between statistically independent events and mutually exclusive events, sampling with and without replacement.
Two events are statistically independent if the first event do not affect outcome of the second event and vice versa. But, these two events may have something in commons called join events. If the two events do not have something in common, then the two events are called mutually exclusive events .
For example, you have a basket with 5 colorful marbles, 2 marbles has Red color, 2 marbles has Green color, and one Blue marble in short [R, R, G, G, B]. Let us do simple experiments called sampling with replacement and sampling without replacement .
Take two of these marbles without replacement, meaning that after you see the color of the first marble you take, record it and immediately take the second marble. Do not return those marbles into the basket. Now, what is the probability that the first marble you take is Red and the second marble is Blue? Since you have 5 marbles in the beginning and 2 Red, then the probability that you get Red first marble is 2 out of 5 = 40%. After the first even, the total marbles in the basket become 4. The probability that you get Blue second marble is 1 out of 4 = 25%. Thus, the probability that you get Red marble then Blue marble is 40% times 25% = 10%.
Now return all marbles in the basket. This time you will take two of these marbles with replacement, meaning that after you see the color of the first marble and record it, return that marble to the basket before you take the second marble. Notice that the total marbles of the two events are constant, equal to 5, because everytime you take a marble, you return it to the basket before you do the next event. What is the probability that the first marble you take is Red and the second marble is Blue? You have 2 red marbles out of 5 = 40% and you have 1 Blue marble out 5 = 20%. Multiply these two percentages, we get 40% times 20% = 8%.
Now the statistical moral story is like this. The two types of sampling has something in common because they are taken from the same sample of 5 marbles in one basket. In sampling without replacement , the first event will affect the second event. We say that the two events are dependent to each other. In the marble experiment, this relation happens because the total sample change (i.e. reduce) after the first event. The probability of taking the next event is depending on the previous event. On the other hand, for sampling with replacement , the first event do not affect the outcome of the second event. We called the two events are statistically independent . In the marble experiment, the total sample never change because you always return the marble that you examine. The probability of taking the next event is not depending on the previous event.
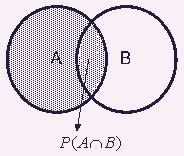
Formally, we say that an event A is independent from event B if the conditional probability is the same as the marginal probability, that is
![]()
or
![]()
What will happen to the intersection (joint probability) when the events are independent?
Using multiplicity rule we have
![]()
Thus, when two events are independent, we get
![]()
I will explain another example using table percentage by total from Conditional Probability section. Before we know the value in the inner cells and get the summation of rows and summation of columns.

Suppose, I preserve the summation of row and summation of column, that is the marginal probability, but empty the inners cells of the table

Now we want to input the inner cells such that the income would an independent event from the car type. What will the values of the inner cells? Because the value of the inner cells represents joint probability, and if the events are independent, the join probability is simply a multiplication of the marginal probability, then we have
![]()
When all the value of inner cells is equal to the multiplication of its sum of rows by its sum of columns, the table has independent joint probability.

Mutually exclusive events do not have joint events. Suppose the table above has all zero inner cells (automatically the sums are also zero), then the two variables of income level and car type are mutually exclusive.

Rate this tutorial & Send your comments, questions and suggestions
See also : Bootstrap sampling
Preferable reference for this tutorial is
Teknomo, Kardi. Data Analysis from Questionnaires. https:\\people.revoledu.com\kardi\ tutorial\Questionnaire\
