Q-Learning Example: Tower of Hanoi

by Kardi Teknomo

Q-Learning e-book

< Previous | Next | Contents >

Read this tutorial comfortably off-line. Click here to purchase the complete E-book of this tutorial

Tower of Hanoi using Q-Learning

To wet your appetite more about this Q learning, I make another simple example on solitary game of Tower of Hanoi . Click here if you want to actually play this game

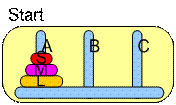
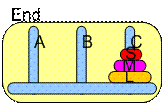
Q-Learning By Examples: Tower of Hanoi Q-Learning By Examples: Tower of Hanoi

We have three towers name A, B and C and 3 disks of different size name S (small), M (medium), and L (large). In the beginning, all the disks are in tower A and the goal is to move the disks, one at a time, so that in the final state all the three disks are in tower C. The constraint is the size of the disk: a smaller disk cannot be put below a larger disk. Thus, you cannot put disk S below M or L, and you cannot put disk M below L.

The game is very simple and the goal is to get the minimum number of disk movement.

Can you think of a solution?

Before going to the solution, let us consider the states of the game. Our simple three disk Tower of Hanoi game may have many states. Can you think of how many states does Tower of Hanoi have?

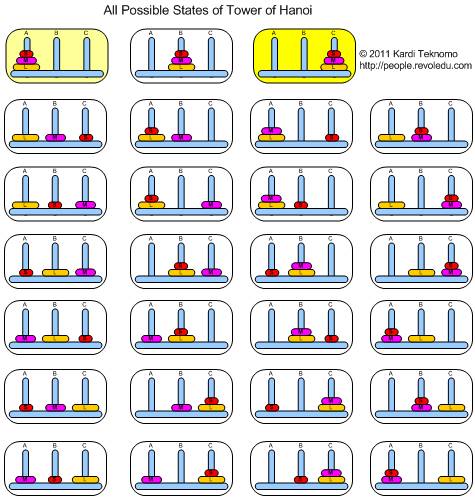
Since the game is rather simple, I found out that the state combinations of tower of Hanoi with 3 disks are 27 states. Here are the 27 states of the tower of Hanoi:


3 disks in a tower

1 disk in a tower

(SL) disks in a tower

(ML) disks in a tower

(SM) disks in a tower

(SML)**
*(SML)*
**(SML)

LMS
LSM
MLS
SLM
MSL
SML




(SL)M*
(SL)*M
M(SL)*
*(SL)M
M*(SL)
*M(SL)




(ML)S*
(ML)*S
S(ML)*
*(ML)S
S*(ML)
*S(ML)




(SM)L*
(SM)*L
L(SM)*
*(SM)L
L*(SM)
*L(SM)




State notation SML represents disk S is in tower A, disk M is in tower B and disk L is in tower C.

Symbol (SML) represents disk S is on top of disk M and both of them are on top of disk L and the parentheses symbol is to indicate that the three disks are located in one tower. The * is to indicate that there is no disk in the tower. Thus, state *(SML)* represents empty tower A and C while tower B contains the three disks.

Similarly, symbol (SM) represents disk S is on top of disk M and the parentheses is to indicate the two disks are located together in one tower. Thus state (SM)L* indicates disk S and M are in tower A, disk L is in tower B and empty tower C.

Diagram below shows all 27 possible state of the Tower of Hanoi. All possible states of Tower of Hanoi

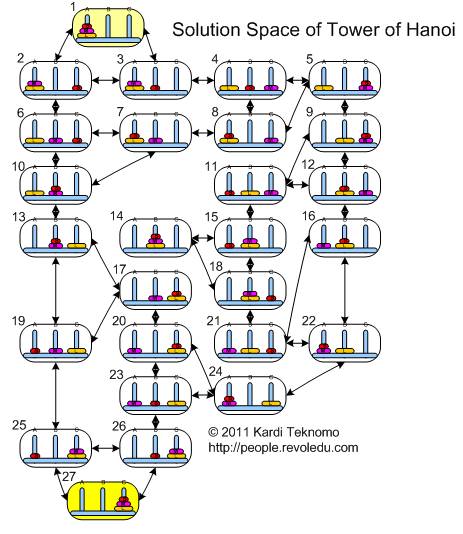
From all possible states, we can create all possible transitions between states. That is our next move. Graph below is my solution. I trace all possible combination of states and all possible combination of transition between states from the starting state until the final state. Let us call the diagram below as the solution space of the tower of Hanoi.


Solution Space of Tower of Hanoi

In the next section, you will learn the solution of the Tower of Hanoi using Q-Learning.

Tired of ads? Read it off line on any device. Click here to purchase the complete E-book of this tutorial

< Previous | Next | Contents >

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. 2005. Q-Learning by Examples. http://people.revoledu.com/kardi/tutorial/ReinforcementLearning/index.html