Chebyshev Distance
Chebyshev distance is also called Maximum value distance. It examines the absolute magnitude of the differences between coordinates of a pair of objects. This distance can be used for both ordinal and quantitative variables.
Other name : Tchebyschev Distance (due to translation)
Formula
![]()
Experiment with the interactive program below. Suppose you need to walk from location A to location B. There are two paths. Using path-1, you need to walk 3 km, while using path 2, you need to walk 4 km. What is the Chebyshev Distance from location A to location B? Put A = (0, 0) to indicate the origin and B = (3, 4), the Chebyshev distance represents the maximum length of walking distance from location A to location B through any paths . If you have the third dimension, it may represent the height and the fourth dimension can represent any other factors such as satisfaction, comfortability, etc.
Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Chebyshev Distance" button. The program will directly calculate when you type the input.
Example
|
|
|
Features
|
|
|
|
|
|
cost |
time |
weight |
incentive |
|
|
Object A |
0 |
3 |
4 |
5 |
|
|
Object B |
7 |
6 |
3 |
-1 |
Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).
The Chebyshev Distance between point A and B is
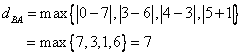
The pattern of Chebyshev distance in 2-dimension is square. When the sink is on the center, it forms concentric squares around the center.

Chebyshev distance is a special case of
Minkowski distance
with
![]() (take a limit)
(take a limit)
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity

