<
Previous
|
Next
|
Contents
>
Variation or Spread of Data
If you notice again your running-time data
you may agree that in general,
any measurement will produce a variation in the data
. However, when you get the last two walking time, the record now become
You may say that the last two data is very special in at least two reasons:
- It happens because you get sick , thus it does not represent your running time record. In fact, they were walking time , not running time .
- By pure chance , the last two data produce exactly the same result up to 1 digit significant. It happens only by accident. If you could repeat again, it may produce different result.
The question now is how to measure the spread or variation of data ?
You may use the interactive program below to compute variation of data in term of
Range
,
Interquartile Range
,
Mean Absolute Deviation
and
Variance & Standard Deviation
. To use the program, type your own data (comma separated numbers) and then click "Get Variation" button.
Range
One way is to measure the range of data, which is maximum value minus the minimum value in the data. Using the true running time (the first six records) the maximum running time is 25.1 seconds and the minimum running time is 17.9 seconds, it give range of 7.2 seconds. The formula of Range is
Interquartile Range
Another way to measure spread of data is by computing the inter-quartile range (IQR), which is the difference between upper quartile
and lower quartile
.
The percentile of data
is computed by sorting the data and take the sample value such that at least
of the values in the data is smaller than or equal to
.
Similar to median , IQR is a robust indicator against outlier, but the computation of percentile require sorting of data which somewhat more complexity.
Deviation
Both inter-quartile range (IQR) and range, however, do not consider the value of central tendency . When we want to measure the spread of data while still considering the value of central tendency, we measure deviation of each data from the central tendency. Suppose we use mean as the central tendency, we have total deviation as
.
This total deviation however, cannot be used to measure the spread because the value is always zero regardless what kind of data we have. Why it become zero? As one nice properties of arithmetic mean, a half of the data have greater value than the mean (produce positive deviation) and the other half are smaller then the arithmetic mean, (produce negative deviation). Interestingly, both sum of positive and negative deviation are at the same values. When we sum the positive deviation and negative deviation, the result is always zero.
To avoid zero total deviation, we have two simple ways: the first one is to take absolute value of each deviation, produce total absolute deviation as
To remove the effect of total number of data, mean absolute deviation (MAD) may give better indicator to measure the spread of data.
The problem with absolute is the discontinuity at the origin (in this case at the central tendency). You may see the discontinuity from the graph of Absolute value
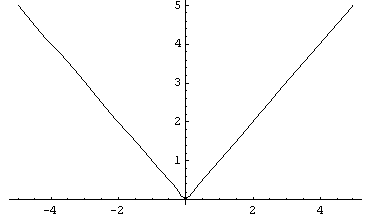
Variance and Standard Deviation
The second way to avoid zero total deviation is by squaring the value of each deviation before take the summation. Again, to remove the effect of total number of data, we divide the sum of square deviation with the number of data to produce average of sum of square deviation
The long name "average of sum of square deviation" has a simple well known name Variance. Variance is a very good indicator to measure the spread of data because variance already consider
- deviation of each data from the central tendency, and
- effect of total number of data, and
- smooth function
However, variance has one weakness: the unit of variance is square of the unit of mean. Your running time data has unit of seconds, the variance has unit of
. To avoid the unit problem, we take the square root of variance and we get what is called
Standard Deviation
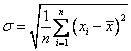
Actually, variance and standard deviation still has one more problem that I did not tell you. When you gather your record of running time, what you did was actually taking sample of your running time. When we calculate the statistics and indicators, what we want to get is the actual population of your real running time. You hope that the sample is good enough to represent the complete population of data such that the statistical indicators that we derive from the sample can represent the population, not just for the sample itself. In other words, we want to inference or generalize our sample as our population. That's what statistics about.
If could take so many samples and take the average of those samples, then the
average of average
would be the real average value of the populations. For single sample, the average value is
. Say we have so many sample data set name
, each of them has average of sample
, then the average of average has notation
. The
is the average of the population.
Now back to our problem in variance and standard deviation. The problem happens when we take the average of sample variance or average of sample standard deviation. The average of sample variance is not the same as population variance. The statisticians call this problem biased variance or standard deviation. To solve this problem and make them the same, we should use this unbiased formula for sample variance
So that the formula of population variance will remain the same as
.
Similarly, the unbiased formula for standard deviation is
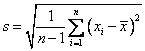
so that the formula of population standard deviation will remain the same as
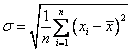
< Previous | Next | Contents >
Rate this tutorial or give your comments about this tutorial
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. Learning from Data. https:\\people.revoledu.com\kardi\ tutorial\Statistics\