Numerical Example of K-Means Clustering

< Previous | Next | Contents >

Tired of ads? Do want to read comfortably this tutorial from any device? Purchase the complete e-book of this k means clustering tutorial .

K Means Numerical Example

The basic step of k-means clustering is simple. In the beginning we determine number of cluster K and we assume the centroid or center of these clusters. We can take any random objects as the initial centroids or the first K objects in sequence can also serve as the initial centroids.

Then the K means algorithm will do the three steps below until convergence

Iterate until stable (= no object move group):

1. Determine the centroid coordinate
2. Determine the distance of each object to the centroids
3. Group the object based on minimum distance

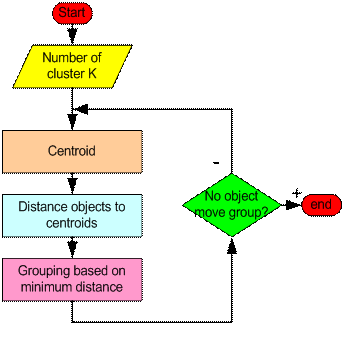
The numerical example below is given to understand this simple iteration. You may download the implementation of this numerical example as Matlab code here . Another example of interactive k- means clustering using Visual Basic (VB) is also available here . MS excel file for this numerical example can be downloaded at the bottom of this page.

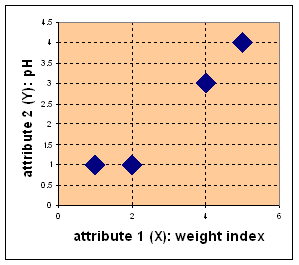
Suppose we have several objects (4 types of medicines) and each object have two attributes or features as shown in table below. Our goal is to group these objects into K=2 group of medicine based on the two features (pH and weight index).

Each medicine represents one point with two attributes (X, Y) that we can represent it as coordinate in an attribute space as shown in the figure below.

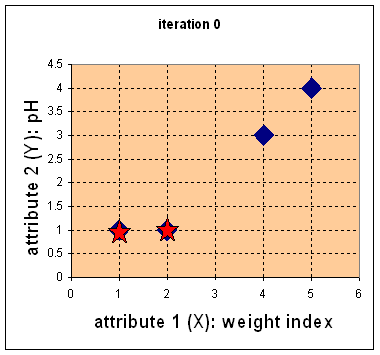
1. Initial value of centroids : Suppose we use medicine A and medicine B as the first centroids. Let and denote the coordinate of the centroids, then and

2. Objects-Centroids distance : we calculate the distance between cluster centroid to each object. Let us use Euclidean distance , then we have distance matrix at iteration 0 is

Each column in the distance matrix symbolizes the object. The first row of the distance matrix corresponds to the distance of each object to the first centroid and the second row is the distance of each object to the second centroid. For example, distance from medicine C = (4, 3) to the first centroid is , and its distance to the second centroid is , etc.

3. Objects clustering : We assign each object based on the minimum distance. Thus, medicine A is assigned to group 1, medicine B to group 2, medicine C to group 2 and medicine D to group 2. The element of Group matrix below is 1 if and only if the object is assigned to that group.

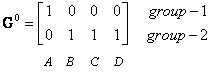
4. Iteration-1, determine centroids : Knowing the members of each group, now we compute the new centroid of each group based on these new memberships. Group 1 only has one member thus the centroid remains in . Group 2 now has three members, thus the centroid is the average coordinate among the three members: .

5. Iteration-1, Objects-Centroids distances : The next step is to compute the distance of all objects to the new centroids. Similar to step 2, we have distance matrix at iteration 1 is

6. Iteration-1, Objects clustering: Similar to step 3, we assign each object based on the minimum distance. Based on the new distance matrix, we move the medicine B to Group 1 while all the other objects remain. The Group matrix is shown below

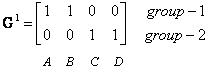
7. Iteration 2, determine centroids: Now we repeat step 4 to calculate the new centroids coordinate based on the clustering of previous iteration. Group1 and group 2 both has two members, thus the new centroids are and

8. Iteration-2, Objects-Centroids distances : Repeat step 2 again, we have new distance matrix at iteration 2 as

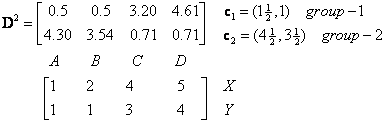
9. Iteration-2, Objects clustering: Again, we assign each object based on the minimum distance.

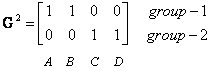
We obtain result that . Comparing the grouping of last iteration and this iteration reveals that the objects does not move group anymore. Thus, the computation of the k-mean clustering has reached its stability and no more iteration is needed. We get the final grouping as the results

Click here to learn about multivariate data ( up to n dimensions) and other type of distances .

Do you have question regarding this k means tutorial? Ask your question here

Note:

Zlatan Aki Mur , an independent AI researcher from Croatia has contributed the MS Excel file based on this example. You may download his example here .

Purchase the complete e-book of this k means clustering tutorial here .

This page has Spanish translation by Jaime Orjuela, an IT Teacher at Escuela Colombiana de Ingeniería

< Previous | Next | Contents >