Analytic Hierarchy Process AHP Tutorial

How to Compute Priority Vetor>

Having a comparison matrix, now we would like to compute priority vector, which is the normalized Eigen vector of the matrix. If you would like to know what the meaning of Eigen vector and Eigen value is and how to compute them manually, go to my other tutorial and then return back here. The method that I am going to explain in this section is only an approximation of Eigen vector (and Eigen value) of a reciprocal matrix. This approximation is actually worked well for small matrix size Priority Vector and there is no guarantee that the rank will not reverse because of the approximation error. Nevertheless it is easy to compute because all we need to do is just to normalize each column of the matrix. At the end I will show the error of this approximation.

Suppose we have 3 by 3 reciprocal matrix from paired comparison

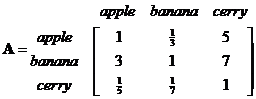
Priority Vector

We sum each column of the reciprocal matrix to get

Priority Vector

Then we divide each element of the matrix with the sum of its column, we have normalized relative weight. The sum of each column is 1.

Priority Vector

The normalized principal Eigen vector can be obtained by averaging across the rows

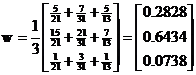
Priority Vector

The normalized principal Eigen vector is also called priority vector . Since it is normalized, the sum of all elements in priority vector is 1. The priority vector shows relative weights among the things that we compare. In our example above, Apple is 28.28%, Banana is 64.34% and Cherry is 7.38%. John most preferable fruit is Banana, followed by Apple and Cheery. In this case, we know more than their ranking. In fact, the relative weight is a ratio scale that we can divide among them. For example, we can say that John likes banana 2.27 (=64.34/28.28) times more than apple and he also like banana so much 8.72 (=64.34/7.38) times more than cheery.

Aside from the relative weight, we can also check the consistency of John's answer. To do that, we need what is called Principal Eigen value. Principal Eigen value is obtained from the summation of products between each element of Eigen vector and the sum of columns of the reciprocal matrix.

Priority Vector

Computation and the meaning of consistency are explained in the next section.

As a note, I put the comparison matrix into Matlab to see how different is the result of numerical computation of Eigen value and Eigen vector compared to the approximation above.

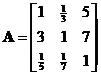
Priority Vector

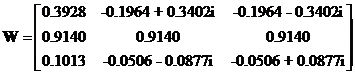
We get three Eigen vectors concatenated into 3 columns of matrix Priority Vector

Priority Vector

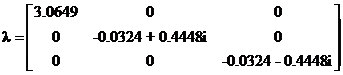
The corresponding Eigen values are the diagonal of matrix Priority Vector

Priority Vector

The largest Eigen value is called the Principal Eigen value, that is Priority Vector which is very close to our approximation (about 1% error). The principal Eigen vector is the Eigen vector that corresponds to the highest Eigen value.

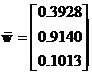
Priority Vector

The sum is 1.4081 and the normalized principal Eigen vector is

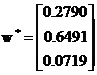
Priority Vector

This result is also very close to our approximation

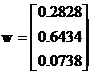
Priority Vector

Thus the approximation is quite good.

Thus the sum of Eigen vector is not one. When you normalized an Eigen vector, then you get a priority vector. The sum of priority vector is one.

In next section you will learn how to make use of information of principal eigen value to measure whether the opinion is consistent.

Click here to purchase the PDF copy of this AHP tutorial

Do you have question regarding this AHP tutorial? Ask your question here

< Previous | Next | Contents >

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2006) Analytic Hierarchy Process (AHP) Tutorial .
http://people.revoledu.com/kardi/tutorial/AHP/