Eigenvalue and Eigenvector
A matrix usually consists of many scalar elements. Can we characterize a matrix by a few numbers? In particular, our question is given a square matrix
, can we find a scalar number 
and a vector 
such that
? Any solution of equation 
for 
is called eigenvector of
. The scalar is called the eigenvalue of matrix
.
Eigenvalue is also called proper value, characteristic value, latent value, or latent root. Similarly, eigenvector is also called proper vector, characteristic vector, or latent vector.
In the topic of Linear Transformation, we learned that a multiplication of a matrix with a vector will produce the transformation of the vector
. Notice the equation 
said that multiplication of a matrix by a vector is equal to multiplication of a scalar by the same vector. Thus, the scalar 
characterizes the matrix
.
Since eigenvalue 
is the scalar multiple to eigenvector
, geometrically, eigenvalue indicates how much the eigenvector
is shortened or lengthened after multiplication by the matrix
without changing the vector orientation.
Algebraically, we can solve the equation 
by rearranging it into a homogeneous linear system 
where matrix 
is the identity matrix order
. A homogeneous linear system has non trivia solution if the matrix 
is singular. That happens when the determinant is equal to zero, that is
. Equation is called the characteristic equation of matrix
.
Expanding the determinant formula (using cofactor), we will get the solution in the polynomial form with coefficients
. This polynomial equation 
is called the characteristic polynomial of matrix
. The solution of the characteristic polynomial of 
are 
eigenvalues, some eigenvalues may be identical (the same eigenvalues) and some eigenvalues may be complex numbers.
Each eigenvalue has a corresponding eigenvector. To find the eigenvector, we put back the eigenvalue into equation
. We do that for each of the eigenvalue. If 
is an eigenvector of A, then any scalar multiple is also an eigenvector with the same eigenvalue. We often use normalized eigenvector into unit vector such that the inner product with itself is one
.
Example:
Find eigenvalues and eigenvectors of matrix
Solution: we form characteristic equation
The eigenvalues are
and
.
For the first eigenvalue
, the system equation is
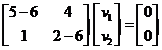
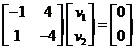
The two rows are equivalent and produces equation
. This is an equation of a line with many solutions, we can put arbitrary value 
to obtain
. You can also write as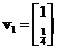 
or 
and they lie on the same line.
The normalized eigenvector is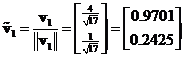 
For the second eigenvalue
, the eigenvector is computed from the system equation 
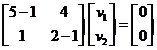
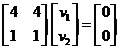
The two rows are equivalent and produces equation
. This is an equation of a line with many solutions, arbitrarily we can put 
to obtain
. You can also write as 
or 
and they lie on the same line.
The normalized eigenvector is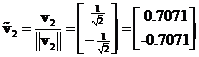
Thus, eigenvalue 
has corresponding eigenvector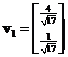
and eigenvalue 
has corresponding eigenvector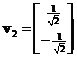
. Note that the eigenvectors are actually lines with many solutions and we put only one of the solutions. They are correct up to a scalar multiple. Since the eigenvalues are all distinct, the matrix is diagonalizable and the eigenvectors are linearly independent.
Properties
Some important properties of eigenvalue, eigenvectors and characteristic equation are:
- Every square matrix has at least one eigenvalue a corresponding non zero eigenvector.
- When a square matrix has multiple eigenvalues (that is repeated, non-distinct eigenvalues), we have two terms to characterize the complexity of the matrix:
- The algebraic multiplicity of an eigenvalue
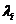is the integer 
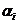associated with 
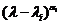when it appears in the characteristic polynomial. If the algebraic multiplicity is one, the eigenvalues is said to be simple. - The geometric multiplicity of
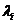is the number of linearly independent eigenvectors that can be associated with
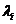. For any eigenvalue, the geometric multiplicity is always at least one. Geometric multiplicity never exceeds algebraic multiplicity.
Example:
Matrix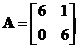
has characteristic polynomial 
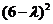thus the eigenvalue is 6 with algebraic multiplicity of 2. There is only one linearly independent eigenvector
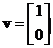, thus the geometric multiplicity is 1.
- The algebraic multiplicity of an eigenvalue
- The eigenvectors that belong to distinct eigenvalues are linearly independent eigenvectors. This is true even if the eigenvalues are not all distinct.
- If a square matrix
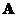has fewer than 
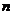linearly independent eigenvector, then matrix 
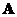is called defective matrix. Defective matrix is not diagonalizable. - When the eigenvalues of a square matrix
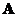are all distinct (no multiple eigenvalues), we called it non-defective matrix. A non-defective matrix has 
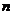linearly independent eigenvectors that can form a basis (i.e. a coordinate system) for 
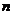dimensional space. Non-defective matrix
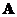is diagonalizable by similarity transformation 
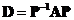into a diagonal matrix 
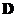. The eigenvalues of 
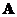lie on the main diagonal of 
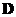. Modal matrix 
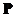is formed by horizontal concatenation of the 
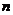linearly independent eigenvectors
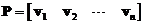. - If matrix
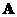is symmetric then matrix 
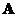has linearly independent Eigen vectors and the Eigen values of symmetric matrix 
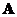are all real numbers (no complex numbers). - If all eigenvalues of symmetric matrix
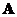are distinct (all eigenvalues are simple), then matrix 
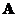can be transformed into a diagonal matrix. Furthermore, the eigenvectors are orthogonal. - Matrix
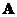satisfies its own characteristic equation. If polynomial 
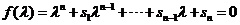is the characteristics polynomial equation of a square matrix A, then matrix 
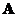satisfies Cayley-Hamilton equation
.
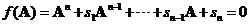Interactive Eigenvalue and eigen vectors below are useful to compute general square matrix. You can select from the matrix example and click 'Compute Eigenvalues and Eigenvectors' button. This is a working progress, thus the result are not perfect yet, sometimes it would still produce inaccurate results.
See also: Matrix Eigen Value & Eigen Vector for Symmetric Matrix, Similarity and Matrix Diagonalization, Matrix Power
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\