Vector Scalar Multiple
Multiplication of a vector
by a scalar
will change the magnitude of the vector
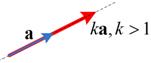
times. The direction of the scalar multiple
is the same as the input vector
if
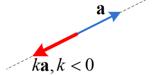
and the opposite direction if
. The magnitude of the scalar multiple is stretched when
and shrink when
.The line of application of the vector does not change, they are collinear (there is no distinction between parallel and collinear in vectors of our definition).
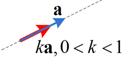
Example
,
, then
,
.
The interactive program below show you algebraic of vector scalar multiple. Your input must be a vector and the program will produce the result of vector scalar multiple.
Properties
Some important properties of vector scalar multiple are
-
Vector scalar multiple is a commutative operation. If you reverse the order you will get the same result
-
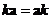
Vector scalar multiple is an associative operation. You can exchange the order of computation (operation inside parentheses are to be computed first) does not change the result
.
-
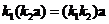Vector scalar multiple is also an associative operation with respect to vector inner product. You can exchange the order of computation without changing the result
.
-
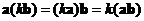Vector scalar multiple is a distributive operation. You can distribute (and group) the scalar with respect to addition
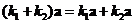and multiplication
.
-
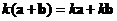When the scalar is zero, vector scalar multiple will produce a zero vector
-
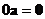
When the scalar is one, vector scalar multiple will produce the input vector itself
-
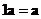
When the scalar is negative one, vector scalar multiple will produce the negative of the input vector
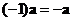
See also : Eigen value & Eigen vector , matrix scalar multiple
Rate this tutorial or give your comments about this tutorial