Symmetric Matrix

By Kardi Teknomo, PhD.

<Next | Previous | Index>

A square matrix is symmetric if its transpose is equal to itself, that is

Symmetric matrix is important in many applications because of its properties. Examples of well known symmetric matrices are correlation matrix, covariance matrix and distance matrix.

You can easily create symmetric matrix either by

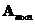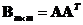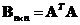1. Multiplying a matrix by its transpose: if is a rectangular matrix, then  and  are symmetric matrices. 
2. Adding a matrix by its transpose: if 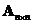is a square matrix, then 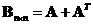 is a symmetric matrix. 

The interactive program below is designed to answers the question whether the given input matrix is a symmetric matrix. When you click “Random Example” button, it will create random input matrix to provide you with many examples of symmetric and non-symmetric matrices. You may also want to try to type your own input matrix to test whether it is a symmetric matrix.

Properties

Some important properties of symmetric matrix are

• Symmetric matrix is always a square matrix
• If 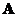is a symmetric matrix order 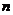 with real entries then
  o   The transpose matrix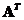 is also a symmetric matrix
  o   Scalar multiple of the matrix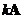  is also a symmetric matrix
  o   The inverse matrix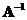 is also a symmetric matrix, if it is invertible.
  o   The inverse of the transpose matrix is equal to the matrix inverse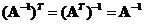
  o   A half of the summation to its transpose produces the matrix itself,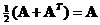
  o   Subtraction to its transpose produces null matrix,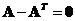
  o   Symmetric matrix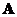has linearly independent Eigen vectors.
  o   The Eigen values of symmetric matrix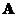 are all real numbers (no complex numbers).
  o   If all eigenvalues of symmetric matrix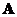 are distinct (no multiple Eigen values), then matrix A can be transformed into diagonal matrix
  o   Eigenvectors of distinct eigenvalues are orthogonal.
  o   The number of non-zero eigenvalues is equal to its rank.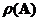
  o   There is an orthogonal matrix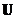 that diagonalizes symmetric matrix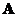by 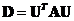 (spectral decomposition).
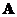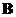• If and  are symmetric matrices of the same size, then
  o   The summation of the matrix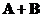 is also a symmetric matrix
  o   The subtraction of the matrix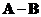 is also a symmetric matrix, if
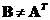
• Let 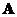be any rectangular matrix size by such that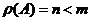, then we can form symmetric matrix 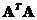and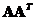. The non-zero eigenvalues of 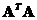and 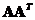are equal. The rank of both matrices are equal, .
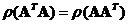• Hermitian matrix 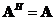is a symmetric matrix with entries of complex number (across the diagonal, the entries are complex conjugate).
• Both Hermitian and Unitary matrix (including symmetric and orthogonal matrix) are called normal matrix because the Eigen vectors form orthonormal set.

See also: Singular Value Decomposition, orthogonal vector, orthogonal matrix, matrix rank, Spectral Decomposition, Symmetric matrix using MS Excel

<Next | Previous | Index>

Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi (2011) Linear Algebra tutorial. http:\\people.revoledu.com\kardi\ tutorial\LinearAlgebra\