Matrix Rank
Recalled in the previous topics when we have a set of basis vectors , we can concatenate these vectors into a matrix. Using this matrix, we can also change the basis or the coordinate system. In this page, you will learn more about that augmented matrix.
Suppose we have a matrix
size
by
. We can imagine this matrix is actually a
vertical concatenation
of row vectors. A set of row vectors that form a matrix is called
row space
of the matrix.
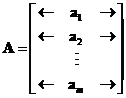
Similarly, we can imagine the matrix
is actually a
horizontal concatenation
of column vectors. A set of column vectors that form a matrix is called
column space
of the matrix.
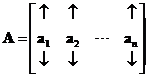
The dimension of row space of a matrix is equal to the dimension of the column space of that matrix. The common dimension of the row space and column space of matrix
is called the rank of matrix
, denoted by
. The rank of
is the number of
linearly independent
vectors and equal to the dimension of space spanned by those vectors. In other words, rank of
is the number of
basis vectors
we can form from matrix
.
Performing elementary row operation does not change the row space. To compute the rank of a matrix, we reduce the matrix into reduced row echelon form (RREF) and non-zero rows of the RREF matrix will form the basis for the row space.
The interactive program below produces matrix rank. The computation is based on numerical method of
Singular Value Decomposition
(SVD). The input is rectangular matrix. Random Example button will provide you with many examples.
Properties
Some important properties of matrix rank are:
-
Transpose
operation does not change the rank of a matrix
.
-
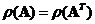Multiplication
of a matrix with its transpose does not change the rank of the matrix
.
-
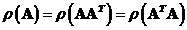Rank of a matrix size
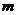by
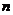is always less or equal to the minimum
size
of the matrix. A matrix is said to be of
full rank
when
.
-
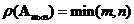Let matrix
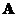and
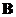both are matrices of the same size
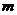by
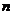, not necessarily of full rank, then we have the following
o Rank of matrix addition :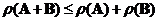
o Rank of matrix subtraction :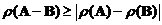
-
Let matrix
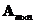and
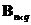are not necessarily the same size, then we have the following
o Rank of matrix product :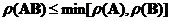
o Rank of matrix product compare to summation of rank: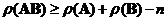
-
The dimension of the
range
and the
null space
of a matrix are related through fundamental relationship
.
-
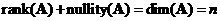A
linear system
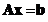has a solution if and only if the rank of the coefficient matrix is equal to the rank of the augmented matrix
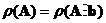. When non-homogeneous system is not full rank or when the rank of the matrix coefficients is less than the rank of the augmented matrix coefficients and the vector constants
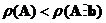then the system is usually inconsistent with no possible solution. It is still possible to find the approximate solution using generalized inverse
.
-
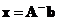A matrix
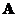has a
left inverse
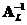if and only if its rank equals its number of columns
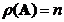. If matrix
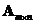has more columns than rows (
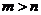), it cannot have a left inverse.
-
A matrix
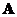has a
right inverse
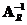if and only if its rank equals its number of rows
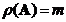. If matrix
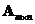has more rows than columns (
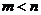), it cannot have a right inverse.
-
A matrix
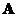has an
inverse
(
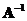non-singular
) if and only if it is a square matrix and the rank of the matrix is full, that is the rank equals to the number of rows (or columns)
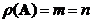. If matrix
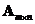is not square (
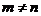), it cannot have a two-sided inverse. Equivalently, the
determinant
of the matrix is non-zero
.
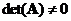See also : rank through RREF , matrix range , matrix nullity and null space , solving system linear equations
Rate this tutorial or give your comments about this tutorial