Linear Algebra tutorial: matrix inverse

Inverse Matrix

When we are dealing with ordinary number, when we say then we can obtain as long as . We write it as or . For example, the inverse of 2 is . Matrix inverse is similar to division operation in ordinary numbers. Suppose we have matrix multiplication such that the result of matrix product is an identity matrix . If such matrix exists, then that matrix is unique and we can write or we can also write .

Matrix inverse exists only for a square matrix (that is a matrix that has the same number of rows and columns). Unfortunately, matrix inverse does not always exist. Thus, we give name that a square matrix is singular if that matrix does not have an inverse matrix (remember a single person does not have a spouse). When a square matrix has an inverse, it is called non-singular matrix .

Because matrix inverse is a very important operation, in linear algebra, there are many ways to compute matrix inverse.

The simplest way to find matrix inverse for a small matrix (order 2 or 3) is to use Cramers rule that employ determinant of the input matrix. Recalled that a square matrix is singular (i.e. no inverse) if and only if the determinant is zero. Matrix inverse can be computed by scaling the adjoint of the input matrix with the determinant, that is 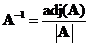. Adjoint of the input matrix is a matrix whose element is the cofactor of the input matrix.
For a 2 by 2 matrix, we can even memorize the formula
When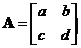 then
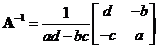
The determinant is set by multiplying the diagonal elements minus the product of the off-diagonal elements and the adjoint is set by reversing the diagonal elements and taking the minus sign of the off diagonal elements.
For matrix of medium size (order 4 to 10), the usage of elementary row operations to produce RREF matrix using Gaussian Elimination or Gauss Jordan is useful.
Other techniques to compute matrix inverse of medium to large size are to use numerical methods such as LU decomposition, SVD , or Monte Carlo method.
For a large square matrix (order more than 100), numerical techniques such as Gauss-Siedel or Jacobi method are used to approximate the matrix inverse.

Example
Find matrix inverse of
Using determinant
We have

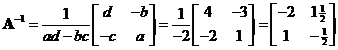
The interactive program below is using numerical methods. As this is an educational program, I limit the matrix size to square matrix of medium size up to order 10. Random Example button will create new random input matrix. The rational output is an approximation of the decimal format.

Properties

Some important properties of matrix inverse are

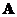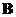If and are square matrices order 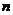and their product produce an identity matrix 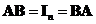, then matrix .
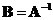If a square matrix 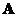has an inverse (nonsingular), then the inverse matrix is unique. There is no other inverse matrix.
A square matrix 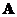has an inverse matrix if and only if the determinant is not zero 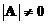. Similarly, matrix 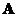is singular (has no inverse) if and only if the determinant is zero .
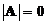A square matrix 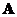order 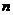has an inverse matrix if and only if the rank matrix is full, that is .
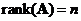If a square matrix 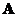has an inverse, the determinant of an inverse matrix is the reciprocal of the matrix determinant, that is .
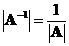If a square matrix 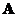has an inverse, and we have a scalar 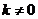then the inverse of a scalar multiple is equal to product of their inverses, that is .
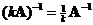If a square matrix 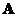has an inverse, the transpose of an inverse matrix is equal to the inverse of the transpose matrix, that is .
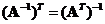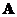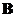If and are square nonsingular matrices order 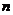then the inverse of their product is equal to the product of their inverse in reverse order, that is .
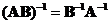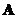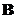Let and are square matrices order 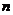. If 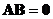then eithe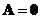r or 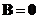or both 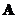and 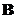are singular matrices (no inverse).