Change of Basis
In this page you will learn how you can transform a point from one coordinate system into another coordinate system.
In the previous topic of
Basis Vector
, you have learned that we can change the coordinate system. Suppose you have a point with coordinate of
in Euclidean space (with standard basis coordinate
and
). We want to find the coordinate of the same point in a new coordinate system form by basis vector
and
. The figure below shows that the new coordinate of the same point is
. In this page, I will show you how you will obtain the coordinate in the new coordinate system.
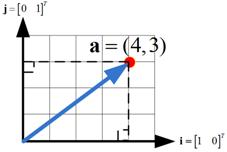
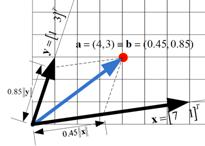
Suppose we start with a point
in the standard Euclidean basis
and
. We want to transform it into a new space
span
by basis vectors
and
. First, we can do
horizontal concatenation
of the new basis vectors into a matrix
. Then, the coordinate of a point in the old basis
is equal to the
matrix multiplication
of the augmented matrix of the new basis
with coordinate of the point in the new basis
. That is
. Thus to get the coordinate of a point in the new basis is the reverse, that is
.
Example:
Our point in the Euclidean basis is
. Our new basis is vector
and
. Augmenting the basis vectors form a matrix
. The
inverse
of the matrix is
. The coordinate of the point in the new coordinate is
.
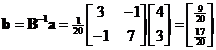Example:
Now suppose we want to find back the coordinate of point
from the coordinate system of basis vectors
and
into Euclidean system.
Augmenting
the basis vectors form a matrix
. We have our coordinate point
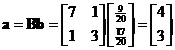back.
Note:
Transformation of coordinate systems follows equality of matrix-vector multiplication
, where
and
are the matrix of the respective basis vectors. In Euclidean coordinate system, the basis vectors form identity matrix
. Thus, the formula
can be simplified into
or
.
See Also
:
Basis Vector
,
Orthogonal Vector
,
Orthogonal Matrix
Rate this tutorial or give your comments about this tutorial