Linear Combination
A set of vectors of
dimensions can be represented as a linear combination of
other vectors. A linear combination of vectors involves both addition and scalar multiplication of vectors.
Span
Geometrically, a set of all linear combination of vectors
generates or
spans
a space. Any point
in that space can be represented as a linear combination of vectors
provided that these vectors cannot be represented as a linear combination of one another. In other words, vectors
span
dimensional space with a minimum number of vectors
such that the only necessary vectors to be included.
Basis Vector
The vectors
are called
basis vectors
because they are the basis of a space. The
space
(or multidimensional space) is indicated by the
coordinate system
. The scalars
are called the
coordinate
because they represent the coordinate of the space. Formally, we say that a
basis
is a set of linearly independent vectors which span the space.
For example
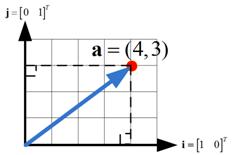
In 2-dimensional Euclidean space (that is the space in an ordinary coordinate system that you have learned since grade school), you represent the coordinate of a point
as a linear combination of the standard unit vectors
.
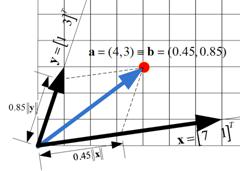
You can represent the same coordinate of a point
as a linear combination of other vectors such as vectors
and
to form
(see Change of Basis to see how we get the coordinate
in the new coordinate system). That is to say that the coordinate of point
in Euclidean coordinate system is
in the new coordinate system. Since the vector
and
form a coordinate system, we call them basis vectors. Notice that the coordinate is the scalar multiple to the length of the basis vector. Coordinate
is
and
is
in the direction of respective basis vectors as shown in the figure below. Notice that the coordinate system does not need to be orthogonal (i.e. perpendicular to each other). Geometrically, the coordinate of a point in the new coordinate system is drawn by taking a parallel line to the basis vectors to cross the other basis vectors.
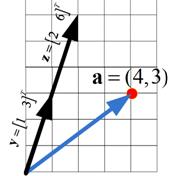
Now let us take a counter example. The same point that we represent in Euclidean coordinate system as
cannot be represented as linear combination of vector
and
. Algebraically, no scalar coordinate can be set to create the linear combination. Thus, the two vectors
and
cannot form a coordinate system. This is because the two vectors are collinear (lie on the same line or parallel lines) as you can see in the figure below. Geometrically, by taking a parallel line to one of the vector you cannot find a crossing point to the other vector.
To form basis vectors, we horizontally concatenate the vectors of the same dimension into a matrix, and then reduce the matrix into matrix RREF . The corresponding columns that contains the leading 1s in the matrix RREF is the basis vectors.
Note:
Suppose we are using vectors of
dimensions (i.e. the vector has
elements) and we have a set of
vectors (
), the set of vector span
dimensional space but any of the vector can be expressed as a
linear combination
of the other
vectors. Thus, the set of vectors is not a basis. By removing the appropriate vectors up to
vectors, we can reduce the set into basis vectors.
Similarly, if we are using vectors of
dimensions (i.e. the vector has
elements) and we have a set of
linearly independent
vectors (
), then the set of vector does not span
dimensional space. Thus, the set of vectors is not a basis. By adding the appropriate linearly independent vectors up to
vectors, we can make the set into basis vectors.
In general, there are two conditions for a set of vectors to form basis vectors:
-
The basis set must have as many basis vectors as the number of dimensions (we say that the basis vector must
span
the space). If the vector length is
dimensions, then we will have
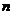basis vectors.
- No basis vector can be put as a sum of the other basis vectors (we say that the basis vectors must be linearly independent).
In short, a set of vectors that can form a coordinate system is called
basis vectors
. Basis vectors are equivalent to
linearly independent
vectors (as long as we keep the number of basis vectors equal to its dimensions
).
In the next topic , you will learn how to test if a set of vectors is linearly independent or linearly dependent vectors.
See Also : Change of Basis , Linearly Independent , Linearly Dependent , Resources on Linear Algebra
Rate this tutorial or give your comments about this tutorial