Matrix Generalized Inverse

By Kardi Teknomo, PhD.

<Next | Previous | Index>

Let us recalled how we define the matrix inverse. A matrix inverse is defined as a matrix that produces identity matrix when we multiply with the original matrix that is we define. Matrix inverse exists only for square matrices.

Real world data is not always square. Furthermore, real world data is not always consistent and might contain many repetitions. To deal with real world data, generalized inverse for rectangular matrix is needed.

Generalized inverse matrix is defined as. Notice that the usual matrix inverse is covered by this definition because. We use term “generalized” inverse for a general rectangular matrix and to distinguish from inverse matrix that is for a square matrix. Generalized inverse is also called pseudo inverse.

Unfortunately there are many types of generalized inverse. Most of generalized inverse are not unique. Some of generalized inverse are reflexive and some are not reflexive. In this linear algebra tutorial, we will only discuss a few of them that often used in many practical applications.

For example:

• Reflexive generalized inverse is defined as
  
  
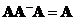
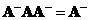
• Minimum norm generalized inverse such that 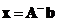will minimizes is defined as
  
  
  
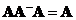
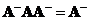
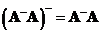
• Generalized inverse that produces least square solution that will minimize residual or error 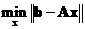is defined as
  
  

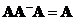
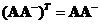
Left Inverse and Right Inverse

The usual matrix inverse is defined as two-sided inverse because we can multiply the inverse matrix from the left or from the right of matrix and we still get the identity matrix. This property is only true for a square matrix.

For a rectangular matrix, we may have generalized left inverse or left inverse for short when we multiply the inverse from the left to get identity matrix. Similarly, we may have generalized right inverse or right inverse for short when we multiply the inverse from the right to get identity matrix. In general, left inverse is not equal to the right inverse.

Generalized inverse of a rectangular matrix is connected with solving of system linear equations. The solution to normal equation is which is equal to. The term is often called as generalized left inverse. Still another pseudo inverse can also be obtained by multiplying the transpose matrix from the right and this is called generalized right inverse.

Moore-Penrose Inverse

It is possible to obtain unique generalized matrix. To distinguish unique generalized inverse from other non-unique generalized inverses, we use symbol. The unique generalized inverse is called Moore Penrose inverse. It is defined using 4 conditions:
1.      
2.      
3.      
4.      

The first condition is the definition of generalized inverse. Together with the first condition, the second condition indicates the generalized inverse is reflexive (). Together with the first condition, the third condition indicates the generalized inverse is the least square solution that minimizes the norm of error. The four conditions above make the generalized inverse unique.

Moore-Penrose inverse can be obtained through Singular Value Decomposition (SVD): such that.

Given a rectangular matrix, the interactive program below produces Moore-Penrose generalized inverse. The Random Example button will generate random matrix. Additionally, the output also include several matrices to let you test the 4 Moore Penrose conditions (,,,) and generalized left inverse or right inverse or matrix inverse depending on the input matrix size. The results can be shown in either rational format or decimal format.

Properties

Some important properties of matrix generalized inverse are

• The transpose of the left inverse of 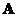 is the right inverse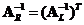. Similarly, the transpose of the right inverse of 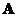  is the left inverse.
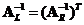• A matrix 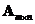has a left inverse 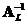if and only if its rank equals its number of columns and the number of rows is more than the number of column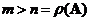.  In this case.
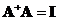• A matrix 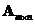has a right inverse 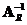if and only if its rank equals its number of rows and the number of rows is less than the number of columns 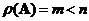 . In this case.
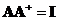• Moore Penrose inverse is equal to left inverse 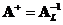when 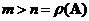and equal to right inverse 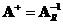when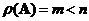. Moore Penrose inverse is equal to matrix inverse 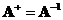when.

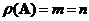See also: Solving System of Linear Equations, Singular Value Decomposition, matrix Inverse, matrix transpose

<Next | Previous | Index>

Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi (2011) Linear Algebra tutorial. http:\\people.revoledu.com\kardi\ tutorial\LinearAlgebra\