Power of a Matrix
A repeat multiplication of a
square matrix
with itself
times produces matrix power
, thus
When the power
is large, computation of matrix multiplication takes a long time and a more efficient method is to transform matrix
into a similar diagonal matrix
using
similarity transformation
. Matrix
(is called modal matrix) is formed by
horizontal concatenation
of the
linearly independent
eigenvectors
. Matrix
can be obtained back from diagonal matrix using
. The computation of matrix power is simplified by taking the power to the scalar diagonal elements. Then multiply the diagonal power with the modal matrix and its inverse
.
When the power
is not integer the computation of matrix power is possible only through similarity transformation into
diagonal matrix
. The
diagonalization
can take place only if the modal matrix
has an
inverse matrix
.
Example:
From matrix
we can obtain diagonal matrix
. Through modal matrix (augmented eigenvectors)
. The inverse modal matrix is
.
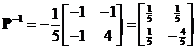Then, matrix power can be computed through repeated matrix multiplication 4 times
. The same result can be obtained using diagonal matrix
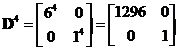. Then we multiply with modal matrix and its inverse, require only three matrix multiplications
.
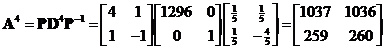Clearly this procedure is only more efficient than matrix multiplication when the power
is large.
However, we have something else that matrix multiplication cannot perform: when matrix power
is not integer.
Example:
Using the matrices in previous example, find
In this example, matrix multiplication cannot solve our problem.
Solution: We can take the exponent to the diagonal elements of the diagonal matrix as in scalar
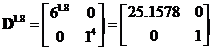. We multiply back to obtain the matrix power
.
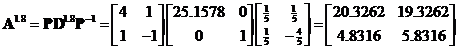See also : Matrix Eigen Value & Eigen Vector , Similarity and Matrix Diagonalization
Rate this tutorial or give your comments about this tutorial