Vector Inner Product
Vector inner product is also called
dot product
denoted by
or
. Vector inner product is also called
vector scalar product
because the result of the vector multiplication is a scalar. Vector inner product is closely related to
matrix multiplication
. It can only be performed for two vectors of the same size.
Geometrically, vector inner product measures the cosine angle between the two input vectors.
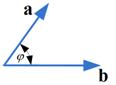
Algebraically, the vector inner product is a multiplication of a row vector by a column vector
to obtain a real value scalar provided by formula below
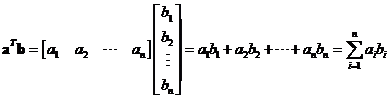
Some literature also use symbol
to indicate vector inner product because the in the computation, we only perform sum product of the corresponding element and the
transpose
operator does not really matter. In this linear algebra tutorial, I use notation
for vector inner product to distinct the inner product from the
outer product
.
Example
Suppose we have
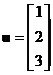and
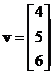, the vector inner product is
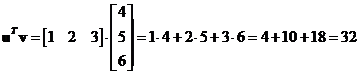
Try the interactive program of Vector Inner Product below. To use the program, simply click the "Vector Inner Product" button. "Random example" button will give you unlimited examples of the vectors in the right format. You can type your own input vectors.
Properties
Some important properties of vector inner product are
-
Vector inner product is a commutative operation. If you reverse the order you will get the same result but you should notice the transpose operator
-
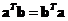
Vector inner product is a distributive operation. You can distribute (and group) the first vector with respect to addition or subtraction
-
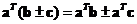
Vector inner product is an associative operation with respect to
scalar multiple of vector
. You can exchange the order of computation (operation inside parentheses are to be computed first) does not change the result
.
-
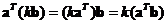Vector dot product to itself always produces positive number except when it is a zero vector
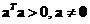. It produces zero if and only if the vector input is a zero vector.
-
Square of Euclidean norm of a vector is equal to the inner product to itself
-
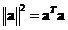
Cosine angle
between two vectors is equal to their dot product divided by the product of their norms
-
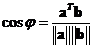
Two vectors are perpendicular (orthogonal) to each other if and only if their inner product is zero
.
-
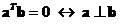Dot product of the same standard unit vector is one
-
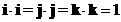
Dot product of the perpendicular standard
unit vector
is zero
-
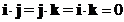
Relationship of
norm
of cross product and dot product is
.
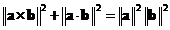See also:
Cross product
,
Outer Product
<
Next
|
Previous
|
Index
>
Rate this tutorial or give your comments about this tutorial