Cosine Angle between Two Vectors
Cosine angle between two vectors is equal to their
dot product
divided by the product of their
norms
.
Example:
Suppose we have
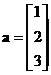and
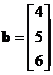, the vector inner product is
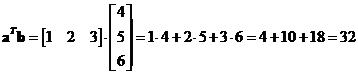
Their norms are
and
.
Therefore, the cosine angle is
and the angle is
.
The interactive program below produces cosine angle between two vectors of the same dimension and also specify the angle in both radians and degrees. Random Example button will generate random vectors at the right format.
Properties
Some important properties of related to cosine angle are
-
Two vectors are
orthogonal
if their dot product is zero
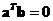, which means the cosine angle is zero
-
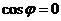
Two vectors are parallel if the absolute value of their dot product is equal to the product of their norms
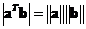, which means the absolute cosine angle is one
.
-
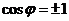Two vectors are in the same direction if their dot product is equal to the product of their norms
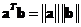, which mean the cosine angle is exactly one
.
-
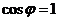Since the value of Cosine is between -1 and +1, the absolute value of vector
dot product
is always less than or equal to the product of their norms
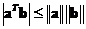. This is called Cauchy-Schwartz inequality.
Rate this tutorial or give your comments about this tutorial