Vector Projection
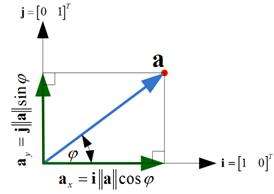
Suppose we have a vector
in 2-dimensional space, and we would like to find the component of vector
in the direction of horizontal and vertical axis. Using trigonometry we can find the magnitude of vector component to be
and
. The direction of these vector components are the standard
unit vector
of horizontal and vertical axes
and
.
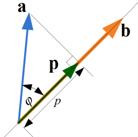
We can find vector projection of a vector
onto other vector
based on the inner product of the two vectors. Scalar projection of vector
onto vector
is the magnitude of projection given as
. Vector projection of vector
onto vector
is the
magnitude
of projection times the
unit vector
of
becomes
. Geometrically, vector projection is shown in the figure below.
Example
Projection of vector
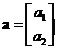onto horizontal axis is equivalent to projection of vector
onto
unit standard vector
. The scalar projection is
. The projection vector becomes
.
Cosine angle
between two vectors is
. Thus,
.
The interactive program below will give you the projection vectors and the scalar projection. You need to provide 2 vectors as the input. Random Example button will generate random input vectors.
Rate this tutorial or give your comments about this tutorial