Evaluation based on Ranks

< Previous | Next | Contents >

Decision Based on Rank

Now we change the value of table 2 into rank.

Table 3: Evaluation based on ranks of each factor

The values of each row are either 1 or 2 or 3 represent the rank (based on the value of previous table). Since smaller rank value is more preferable than higher rank, we need to normalize the sum in different way using formula below

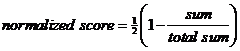
The total sum is 23 (=11+6+6). In this case the normalized score of Choice X is 0.5*(1-11/23) = 26.09%, while the normalized score of Choice Y and Z are 0.5*(1-6/23) = 36.96%. In this case higher normalized score correspond to higher preference. You may notice that we have transformed the rank values (which is ordinal scale) into normalized score value (which is a ratio scale).

Comparing the results of two tables above show that the rank of preference change by the way we compute our case. Even though we based our judgments on the same score values, the rank reduce some information of these values. In this case choice Y and Z become indifference, or equally preferable.

Now let us see what happen if we transform the score value of each factor in such a way such that all factors have the same range value. Say, we choose all factors to have range to be 0 to 1. To convert linearly the score of each factor from table 2 into table 4, we use the following formula which is based on simple geometric of a line segment

The geometry of the linear transformation is shown in the figure below

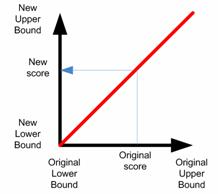
Table 4: Converted New Scores based on Range

For instance, Factor A has originally range 0 to 5. To make score of choice Y from 4 into a range of 0 to 1 we have olb = 0, oub = 5, nlb = 0, nub = 1, and score = 4, thus

. Another example, for choice X in factor B has original score of 20 and original range 1 to 100. Thus we have olb = 1, oub = 100, nlb = 0, nub = 1 and score = 20, thus

Clearly the transformation of score value is a little bit more complicated than rank but we get better results.

In the next section you will learn more general method.

Click here to purchase the e-book copy of this AHP tutorial .

See Also: Rank Reversal

Do you have question regarding this AHP tutorial? Ask your question here

< Previous | Next | Contents >
Comments for this tutorial

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2006) Analytic Hierarchy Process (AHP) Tutorial .
http://people.revoledu.com/kardi/tutorial/AHP/