<
Previous
|
Next
|
Contents
>
Fundamental Relationship between Averages
Time-average , delayed-average , moving-average and delayed-moving-average have several interesting relationships.
Relationship of Time-Average and Moving-average
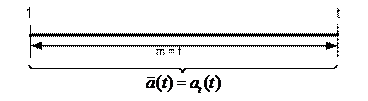
When we set the length of kernel equal to the length of the sequence, that is
, the moving-average is equal to the time-average (tag=movag)
(13)
Proof:
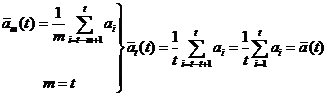QED
Relationship of Delayed-Average and Delayed-Moving-average
If we set the kernel length of delayed-moving-average into
, the delayed-average is equal to the delayed-moving average (dag=demovag)
(14)
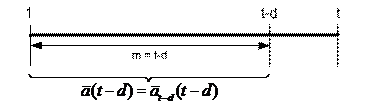
Proof:
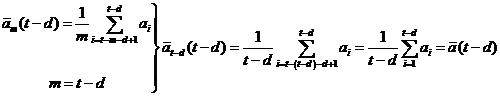QED
Relationship of Delayed-Average and Moving-average and Time-Average
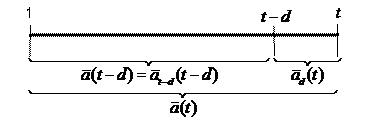
From the average decomposition diagram (ADD), we can decompose the average of whole sequence into two parts of weighted averages
(15)
I call Equation (15) as the fundamental theorem of average : time-average is equal to the sum of length-weighted delayed-average and moving-average.
Proof:
Multiply both side of equation (15) with
we have
(15a)
Expanding the right hand side of equation (15a) we have
QED.
From equation (15) we can derive what I call as Shift Property of Average
(16)
Notice that the right hand side of (16) is evaluated for time
while the left hand side is evaluated at time
Based on equation (15), we can also derive a ratio of difference. The ratio between the difference of moving average to delayed average and the difference of average to delayed average is equal to the ratio between the delay and the length of sequence in consideration. (relationship of movag, dag and tag)
(17)
Proof:
Taking the difference of average and delayed-average multiplies by its own length, we have
because
.
Expand the second term in the left hand side and put the right hand side to the left we get
Gather the same terms
Then,
QED
Relationship of Delayed-Average and Delayed-Moving-Average and Time-Average
We can also decompose the measurement sequence into three parts of length-weighted averages
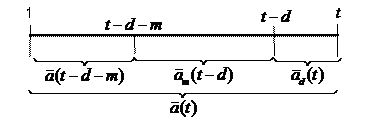
From the average decomposition diagram (ADD), we can decompose
(18)
Combining equation (15) and (18) we have
Removing redundant last term of both side gives
(19)
Equation (19) is the relationship of delayed-average, time average and delayed moving average
Rate this tutorial or give your comments about this tutorial