Prime Factor Using Spreadsheet
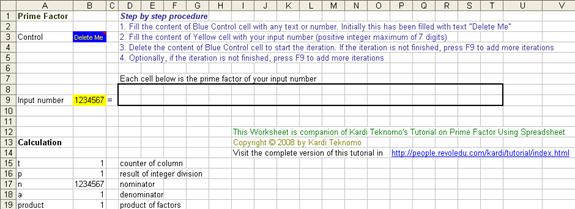
Knowing the algorithm, now we proceed with how we will use spreadsheet iteration (MS Excel 1993/1997) to calculate prime factor of any positive number (we limit ourselves up to 7 digits). Spreadsheet companion of this tutorial can be downloaded here . It's free of charge. The programming challenge is to make a Do-While loop in parallel cells without real loop.
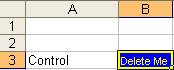
1. We set up a control cell. Suppose cell B3 will be used as control cell. We will fill this cell with any value or text (for example we put text "Delete Me" on it) and color the cell blue such that user can distinguish it. We also give name to this cell by menu Insert > Name > Define > "Control"
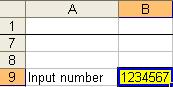
2. We prepare a cell for input number and color it as yellow. We name it
. For example, we set cell B9 as input cell.
3. Now we prepare the cells to actually show the prime factors. Say we want to have a maximum of 17 prime factors (you can do more factors or less factors). Thus, we occupy cell D8 to T8 for the counter of the columns representing the prime factor. We put 1 on D8 and put a formula of =+D8+1 on E8 and copy this formula from F8 to T8. For temporary, we just fill all cells from D9 to T9 with 1. You will end up with the following figure.
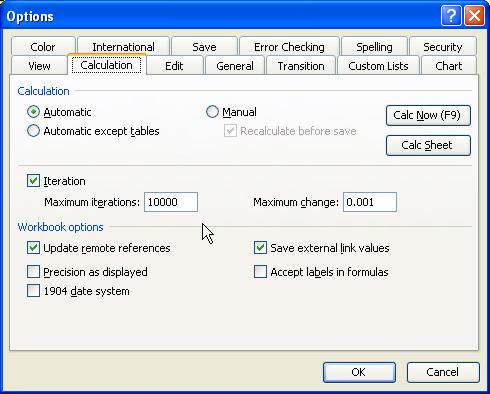
4. The actual computation of prime factor will use iteration. Thus we set menu Tools > Options ?> Calculation Tab > click Iteration Checkbox and set maximum iterations to say 10,000.
5. For the computation part, we set up 5 cells in B14 to B18 and name them respectively
for the counter of column,
for the result of integer division,
for the nominator,
for denominator and
for the product of the prime factors so far.
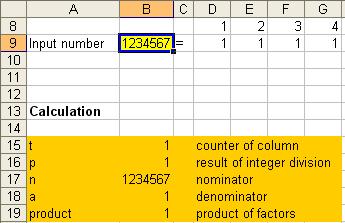
6. Product of all prime factors is put in cell B18
=+PRODUCT(D9:T9)
This product will be used to examine if all the prime factors has been computed.
7. Our original number has name
and we would like to repeatedly divide this number with the smallest prime number. First, we need to give another name for
(or copy the value in another cell) such that after division, the result of division would be our number and will not affect the value of
. Let us call our number
to indicate nominator of division. Thus, we set
for the initial condition (that is if the control cell is not empty). The result of division (which is also
) will be used again for further division if it is divisible. The division take place only if our number
is divisible by our smallest prime factor name
(= cell B17). We use modulus function (MOD) to examine
is divisible by
(that is to set equal to zero). Therefore, the result of division also has the same cell name of
(= cell B16) and we put all of these things together by typing in cell B16
=+IF(Control="",IF(MOD(n, a)=0,n/a,n),v)
The formulas above shall be explained as follow:
If control cell is empty then
If
then
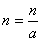
Else,
Do not change
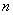
End If
Else
Let
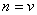
End If
8. Our next computational cell is to find the smallest prime factor. Let us name this cell
in cell B17, type
=+IF(AND(Control="", product<>v),IF(p=1,a+1,1),1)
The formula above can be explained as follow:
If control cell is empty and
of all prime factor is not the same as our original number then
If
is not divisible by
(therefore,
) then
Increment
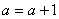
Else,
Set
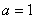
End If
Else
Set
(for the first time)
End If
9.
The next computational cell is actually a transitional cell to show the result of integer division, before we copy this result into the appropriate cell. Let us name this transitional cell as
and locate this in cell B16:
=+IF(Control="",IF(MOD(n,a)=0,a,1),1)
The meaning of this formula is quite straightforward. If our number
is divisible by our smallest prime factor
then we set
, otherwise we set
as our default value.
10. Then we need a counter of column number where we can copy our smallest prime factor into the correct cell. Let us call this variable
and locate it in cell B15:
=+IF(Control="",IF(n=1,0,IF(AND(n>1,p>1),t+1,t)),1)
In here we set initial column number as one if the control cell is not empty. If the control cell is empty, we examine if the loop have been finished. The loop would finish if the product of all prime factor is the same as our original number (that is equivalent to
). In this case, we make agreement to set
to indicate the loop is finished. Otherwise, we need examine if the computation still going on (that is indicated by
). There are two cases in the on going computation:
The transitional cell
The transitional cellindicates we just copy the transitional value of smallest prime factor
into the appropriate cell
indicates we just copy the value of smallest prime factor
into
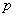
You can see this clearly if you set the Maximum Iteration to 1 instead of 10,000.
11. Finally, we type the following to copy the value of smallest prime factor
into the appropriate cell in cell D9:
=+IF(Control="",IF(t=D$8,p,IF(OR(D9>1,t=0),D9,1)),1)
The meaning of above formula is simply to copy the value of
if the column counter
is equal to the column number above this cell. Otherwise, there are three cases:
-
By our agreement if
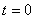, the computation is finished and we keep the value of the cell.
- Alternatively, if the value of this cell has been filled (therefore it is greater than 1), we also want to keep the value of the cell.
- Otherwise, we just set the value of this cell as one.
After that we copy the formula from cell D9 to E9:T9
12. We do conditional formatting such that the column number and cells with value smaller or equal to 1 would be painted with white. We make it colorful and nicer table. The final result is shown below. How to use the spreadsheet is also remarked in the spreadsheet notes.
