Sieve of Erastosthenes
To find out prime number manually the procedure of Sieve of Erastosthenes (275-194 BCE) is used. First, list all integers say 1 to M. Then we repeatedly delete all numbers that divisible by consecutive prime numbers except that prime number itself. We continue the deletion until there is no more composite integers within 1 to M. The remaining numbers are the prime numbers.
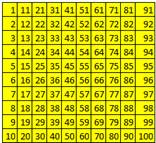
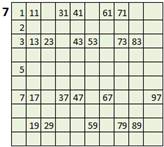
For example, we set M = 100. Since composite integer is divisible by a prime not exceeding its square root, we only need to divide by prime number less than 10, which are 2, 3, 5 and 7. Notice that number 1 is still inside the sieve of Erastosthenes.
|
List integer 1 to 100 |
Delete integers divisible by 2 except 2 |
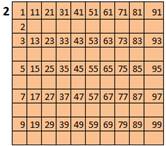
Delete integers divisible by 3 except 3 |
|
|
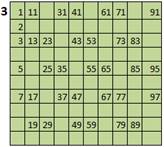
Delete integers divisible by 5 except 7 |
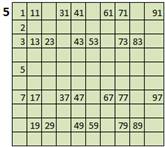
Delete integers divisible by 7 except 7. Now the sieve contain prime between 1 to 100 except 1. |
The following online program will let you play around while learning. This interactive Sieve of Erastosthenes program determines prime list between N1 and N2. With this handy tool, you can challenge yourself to answer these questions:
- How many primes between 10000 and 100000?
- What is the upper bound N2 to get exactly the first 400 primes?
- Is 123456789 prime?
- What is the largest prime using digit 1 to 9? Using digit 0 to 9?
The interactive Sieve of Erastosthenes program below determines prime list between N1 and N2.
If you like these tools recommend them to your friends and tell also to your teachers.
In the next section , you will learn how to find prime number in a code.