Click here to purchase the complete E-book of this tutorial
Distance Matrix
To illustrate hierarchical clustering algorithm, let us use the following simple example. Suppose we have 6 objects (with name A, B, C, D, E and F) and each object have two measured features (X1 and X2). We can plot the features in a scattered plot to get the visualization of proximity between objects.
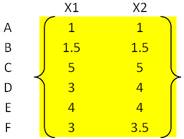
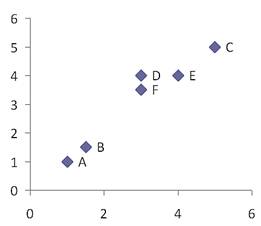
The proximity between object can be measured as distance matrix. Suppose we use Euclidean distance , we can compute the distance between objects using the following formula
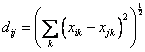
For example, distance between object A = (1, 1) and B = (1.5, 1.5) is computed as
Another example of distance between object D = (3, 4) and F = (3, 3.5) is calculated as
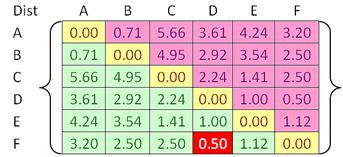
Using the same way as above examples, we can compute all distances between objects and put the distances into a matrix form. Since distance is symmetric (i.e. distance between A and B is equal to distance between B and A), we can focus only on the lower or upper triangular matrix (green or pink part). The diagonal elements of distance matrix are zero represent distance from an object to itself.
In general, if we have m objects, the number of distances on the lower triangular matrix (green part of the distance matrix) contain
number of elements. In our example, we have 6 objects, thus the total distances that need to be computed is
. We listed again below the 15 elements of distances as an array. Clearly the minimum distance is 0.5 (between object D and F).
If the objects contain not only numerical features, you can compute the distance using other type of distances and aggregate multivariate distance. See my Similarity tutorial to get more detail on how to compute other type of distances and multivariate distance.
Having a distance matrix, now we are ready to compute linkages between objects as explain in the next section .
Click here to purchase the complete E-book of this tutorial
Do you have question regarding this Clustering tutorial? Ask your question here
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2009) Hierarchical Clustering Tutorial. http://people.revoledu.com/kardi/tutorial/clustering/