What is Complex Number?
To understand where Complex Number is located in Number Theory, here is a tree diagram.
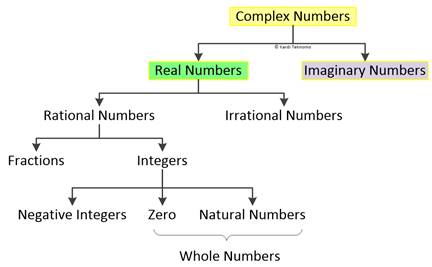
Complex Number is the most general set of numbers that cover all numbers. All numbers are Complex Numbers.
Complex Number consist of 2 parts:
1. Real part
2. Imaginary part
When the imaginary part is zero, we have only the real part, thus we have Real Numbers. In other words, Real Number is a subset of Complex Number.
Real Number consists of Rational Number and Irrational Number. Rational Number consist of Integers and Fractions. Integer consists of Positive Integers and Negative Integer and Zero. (Similarly Fraction can also be seen as positive and negative but I do not show in the diagram above). The set of Positive Integers is also called Natural Numbers. Set of Positive integers and zero is called Whole Numbers.
You see that the imaginary part of Complex Numbers is the distinguished term between Complex Numbers and purely Real Numbers. Let us define a special imaginary operator denoted as
to be
.
Thus, we can also define it as
A complex number
is defined as
.
The real part is
.
The imaginary part is
. Note that the imaginary part by itself, without the imaginary operator
, is a real number.
When the imaginary part is zero, we only have the real part and we write it as
instead of
. When the real part is zero, we write it as
instead of
.
See Also : Euler Formula , Complex Plane , Magnitude and Direction
Rate this tutorial or give your comments about this tutorial