Click here to purchase the complete E-book of this tutorial
Measuring Impurity
Given a data table that contains attributes and class of the attributes, we can measure homogeneity (or heterogeneity) of the table based on the classes. We say a table is pure or homogenous if it contains only a single class. If a data table contains several classes, then we say that the table is impure or heterogeneous. There are several indices to measure degree of impurity quantitatively. Most well known indices to measure degree of impurity are entropy, gini index, and classification error. The formulas are given below
![]()
![]()
![]()
Example
All above formulas contain values of probability of
![]() a class j.
a class j.
In our example, the classes of Transportation mode below consist of three groups of Bus, Car and Train. In this case, we have 4 buses, 3 cars and 3 trains (in short we write as 4B, 3C, 3T). The total data is 10 rows.
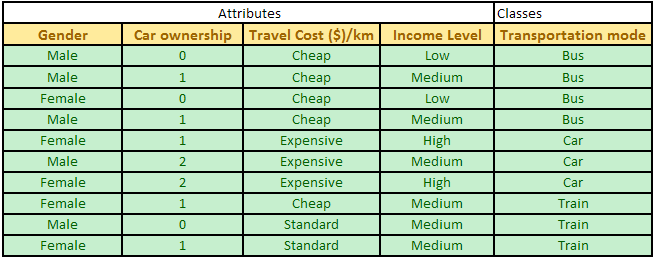
Based on these data, we can compute probability of each class. Since probability is equal to frequency relative, we have
Prob (Bus) = 4 / 10 = 0.4
Prob (Car) = 3 / 10 = 0.3
Prob (Train) = 3 / 10 = 0.3
Observe that when to compute probability, we only focus on the classes , not on the attributes . Having the probability of each class, now we are ready to compute the quantitative indices of impurity degrees.
Entropy
One way to measure impurity degree is using entropy.
![]()
Example: Given that Prob (Bus) = 0.4, Prob (Car) = 0.3 and Prob (Train) = 0.3, we can now compute entropy as
Entropy = - 0.4 log (0.4) ? 0.3 log (0.3) ? 0.3 log (0.3) = 1.571
The logarithm is base 2.
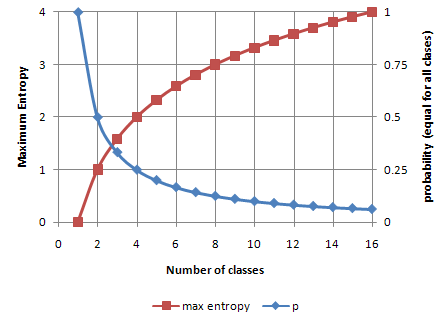
Entropy of a pure table (consist of single class) is zero because the probability is 1 and log (1) = 0. Entropy reaches maximum value when all classes in the table have equal probability. Figure below plots the values of maximum entropy for different number of classes n, where probability is equal to p=1/n. I this case, maximum entropy is equal to -n*p*log p. Notice that the value of entropy is larger than 1 if the number of classes is more than 2.
Gini Index
Another way to measure impurity degree is using Gini index.
![]()
Example: Given that Prob (Bus) = 0.4, Prob (Car) = 0.3 and Prob (Train) = 0.3, we can now compute Gini index as
Gini Index = 1 ? (0.4^2 + 0.3^2 + 0.3^2) = 0.660
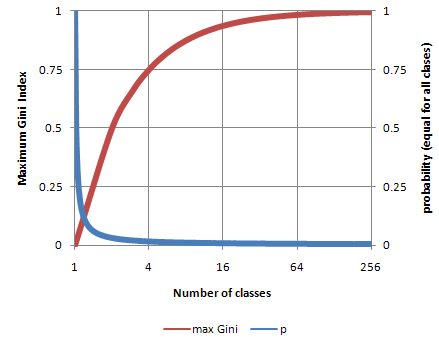
Gini index of a pure table (consist of single class) is zero because the probability is 1 and 1-(1)^2 = 0. Similar to Entropy, Gini index also reaches maximum value when all classes in the table have equal probability. Figure below plots the values of maximum gini index for different number of classes n, where probability is equal to p=1/n. Notice that the value of Gini index is always between 0 and 1 regardless the number of classes.
Classification error
Still another way to measure impurity degree is using index of classification error
![]()
Example: Given that Prob (Bus) = 0.4, Prob (Car) = 0.3 and Prob (Train) = 0.3, index of classification error is given as
Classification Error Index = 1 ? Max{0.4, 0.3, 0.3} = 1 - 0.4 = 0.60
Similar to Entropy and Gini Index, Classification error index of a pure table (consist of single class) is zero because the probability is 1 and 1-max(1) = 0. The value of classification error index is always between 0 and 1. In fact the maximum Gini index for a given number of classes is always equal to the maximum of classification error index because for a number of classes n, we set probability is equal to p=1/n and maximum Gini index happens at 1-n*(1/n)^2 = 1-1/n, while maximum classification error index also happens at 1-max{1/n} =1-1/n.
Knowing how to compute degree of impurity, now we are ready to proceed with decision tree algorithm that I will explain in the next section .
Click here to purchase the complete E-book of this tutorial
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2009) Tutorial on Decision Tree. http://people.revoledu.com/kardi/tutorial/DecisionTree/

