<
Previous
|
Next
|
Contents
>
Solution of Affine Difference Equation
We can classify the solution of difference equation
(linear first order difference equation with constant input) into 10 types and any such difference equation must have a solution that is one of these ten types. There is never more than one type of solutions. By merely examining a difference equation, we will be able to decide which type of solution it has. Moreover, we can make such a statement without the necessity to solve the equation.
The ten possible types of solutions are sorted in the next table .
How does it come out into only 10 possible type of solution? Here is the explanation.
Consider affine dynamical system
It is possible to divide the value of
into six cases:
The only possibility not covered by these six cases
is
that is not allowed in any case if
Equation (1)
is to be a difference equation. Each of these six cases will be divided into three sub cases. Except for
, the three sub cases will be
This will cover all possibility of initial value
. The comparison of
with
comes from the value in the parenthesis of the solution in
Equation(2)
Though it has 6 by 3 = 18 possibilities, there are only 10 possible behaviors of the solutions because some of them are overlapped. The strategy to find the identical solution is as follow:
-
Look at the solutions given in
Equation (2)
that do not involve
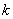at all. This is accomplished by choosing
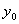so that the coefficient of
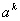is zero (sub case a). Since no
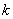appears in the solutions, the solutions do not change as the
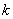changes. Thus the solution is constant.
-
Consider cases when the coefficient of
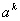is positive (sub case b). After that we observe the behavior of
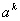as
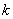get larger.
-
Examine cases when the coefficient of
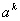is negative (sub case c). After that we inspect the behavior of
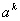as
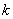get larger.
For case
, instead of choosing
, we choose the value of
(positive, zero and negative).
|
No |
Cases |
Type of Solution |
|
1 |
|
Constant |
|
2 |
|
Exponentially increasing without bound |
|
3 |
|
Exponentially decreasing without bound |
|
4 |
|
Constant |
|
5 |
|
Linearly increasing without bound |
|
6 |
|
Linearly decreasing without bound |
|
7 |
|
Constant |
|
8 |
|
Exponentially decreasing to a bound |
|
9 |
|
Exponentially increasing to a bound |
|
10 |
|
Constant |
|
11 |
|
Oscillating with decreasing amplitude |
|
12 |
|
Oscillating with decreasing amplitude |
|
13 |
|
Constant |
|
14 |
|
Oscillating with constant amplitude |
|
15 |
|
Oscillating with constant amplitude |
|
16 |
|
Constant |
|
17 |
|
Oscillating with increasing amplitude |
|
18 |
|
Oscillating with increasing amplitude |
Step by step to determine the solution of first order linear difference equation
- Put the equation into form of Equation (1 ).
-
Determine
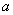and
-
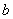
Using the value of
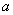, determine which of the six cases cover this equation
-
If
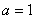, the value of
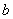compare to
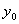will determine the sub case
-
If
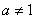, the value of
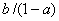compare to
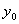will determine the sub case
<
Previous
|
Next
|
Contents
>
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Difference Equation Tutorial. https:\\people.revoledu.com\kardi\ tutorial\DifferenceEquation\