Significant of Digital Root

By Kardi Teknomo, PhD.

< Previous | Next | Contents >

To understand the significant of digital root pattern, in this section, you will learn some applications of digital root. The first few examples are just for fun and then we discuss more serious and practical applications of digital root.

Guess a Digit

Consider to play this guess-a-digit game with one of your friend

1. Ask your friend to write a positive integer number and write it down so that you can see this number (for example, the number she wrote was 1329351)
2. Ask her to take out one digit of any arbitrary location from that number so that you will guess later without telling you which digit she chose. Let her write this digit and hide it from you (suppose she choose to take out the fourth digit, that is 9, but she did not tell you about it)
3. Ask her to sum the remaining digit and report to you only the sum. (she counted the sum as 1 + 3 +2 + 3 + 5 + 1 = 15, and tell you that the sum is 15)
4. Then you did simple calculation and you guess the digit she hide was 9

"How you did that?" she exclaimed on the accuracy of your guess. The secret lies on digital root.

The sum of the number 1329351 is 1 + 3 + 2 + 9 + 3 + 5 + 1 = 24 and the digital root of 24 is 2+4 = 6, while the sum she report to you was 15 with digital root of 1+5 = 6. Since the subtraction of two digital roots was 6 - 6 = 9 then you guess. Hey, how could 6 – 6 is 9? Read on this article and you will understand what it means.

Mind Reader

Here is another fun trick using based on digital root. Play this with your friend to amaze him/her.

1. Write down in a piece of paper number 0. Do not show the number to your friend and put that piece of paper under a book. Just tell your friend that you can read his/her mind.
2. Ask your friend is to tell you a 3 to 5 digit number without telling you what that number is
3. Ask him/her to shuffle the digit of that number again, without telling you what the new number is
4. Ask him/her to take the difference between the two numbers in such a way that the larger number subtracts the smaller number to get positive result
5. Ask him/her to divide the result of subtraction with 9
6. Ask him/her to tell the remainder of division
7. Now ask him/her to open the piece of paper that contains the answer.

Here is the numerical example. Suppose your friend tells you her 5 digit number is 95345. Then the shuffle the digit of that number is 59435.
The difference of the two numbers is 95345-59435=35910
The division by 9 is 35910/9=3990 with reminder 0.

No matter what the number is, the difference between two numbers taken from the permutation of the same number can always be divided by 9. This trick comes from the fact that any number is congruent modulo 9 to its digital root.

Numerology

Ask the client to tell his or her full name.
For each letter of the name assign a number 1 to 9 like this:

Sum the number assigned and get the digital root of that number.
Based on the digit root, you will assign the prediction of character or personality traits or future prediction or horoscope. Of course, the assignment is arbitrary and not true. This is just to show that digital root is also useful for fun and entertainment.

Thus, if the name is Kardi Teknomo, then the assignment would be

The sum of 2+1+9+4+9 + 2+5+2+5+6+4+6 = 55
The digit root of 55 is 1.

Knowing the digital root, then assign to one of the personality. Example of Personality portrait (from Methamusements by Raymond Blum, 1997)

1. There is no one else like you. You are natural leader. Originality and independence are two of your strengths. You have courage to try new things
2. You are kind and gentle. People say that you are considerate and sensitive to the feeling of others. You are the best friend anyone could have. Writing poetry comes naturally to you.
3. You are the life of the party. Center stage is where you feel right at home. You have a great sense of humor. Your true talents are found in art and writing.
4. People can count on you to get things done. You always work hard to achieve your goals. Endless patience and self-discipline are your strengths. You are very loyal to your friends.
5. You are very intelligent. Travelling to far-off places interests you. You are very curious and love to investigate new things. Risk taking is one of your strengths.
6. You have strong moral values. People know that they can trust you and that you are honest. You set the example for everyone else. Helping and caring for others are two of your strong points.
7. You are very smart for your age. Solving mysteries interests you. You have strong love of nature and animals. You are thinker and like to spend time by yourself.
8. You have the power to succeed and you are always organized. Management and authority are two of your strengths. Making money comes naturally to you. An executive position is in your future.
9. Current events interest you. You are always working to help everyone else. Human right is something that you are concerned about. Kindness and understanding are two of your strong points.

Validating Multiplication

We can use digital root to check the correctness of multiplication.

Can you check whether this multiplication is correct or not?
12345 * 3451 = 42672595

Let us examine the digital root of the left hand side of the equal sign. The digital root of 12345 is 6 and the digital root of 3451 is 4, the multiplication of 6*4=24, and the digital root of 24 is 6. Next we examine the digital root of the right hand side of the equal sign. The digital root of 42672595 is 4 and not equal to digital root of the left hand side which is 6. Thus, the multiplication above is incorrect.

Fibonacci Sequence

Fibonacci number is a sequence of numbers obtained by adding two numbers in the sequence recursively. We start with F(1) = 1 and F(2) =1 and we get the next Fibonacci number by adding the last two numbers:

F(1) = 1
F(2) = 1
F(3) = F(2) + F(1) = 1 + 1 = 2
F(4) = F(3) + F(2) = 2 + 1 = 3
F(5) = F(4) + F(3) = 3 + 2 = 5
F(6) = F(4) + F(3) = 5 + 3 = 8
and so on

This addition may be very simple problem but when the numbers are quite large, the addition of two numbers may produce computation error in the computer.

For example,

F(72) = 498454011879264
F(73) = 806515533049393
F(74) = F(73) + F(74) = 1304969544928657

But when you use spreadsheet like Microsoft Excel, for example, you will get

F(74) 1304969544928660

You may not aware of this inaccuracy just by looking at numbers. This kind of inaccuracy is due to round off error and can be detected easily using the pattern of digital root.

The digital root pattern of Fibonacci sequence has 24 digits length cycle: 1-1-2-3-5-8-4-3-7-1-8-9-8-8-7-6-4-1-5-6-2-8-1-9 . After 24 digits, the pattern of digital root repeats itself (see figure below). You can download the MS Excel companion of this article here

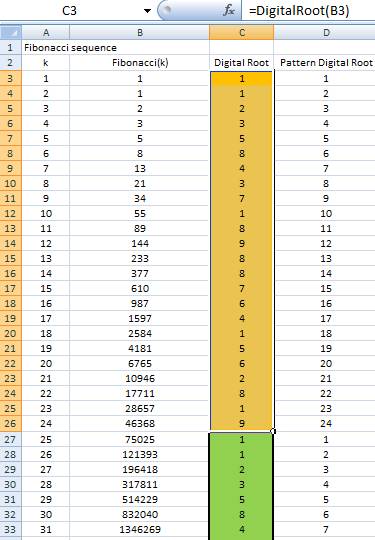
Knowing this cyclical pattern, we shall expect the pattern repeat itself for large Fibonacci number. However, starting from F(74) the pattern of digital root does not repeat itself.

For example,

Digital root of F(72) = 9
Digital root of F(73) = 1
Digital root of F(74) supposed to be 1

But when you use spreadsheet like Microsoft Excel, for example, you will get

F(74) 1304969544928660 (digital root = 4)

After 9-1 pattern in F(72) and F(73), the digital root should be 1 in F(74) but the Excel shows that the digital root of F(74) = 4 which breaks the cyclical pattern of digital root. Thus, digital root is a great help to detect the round off error that Microsoft Excel does.

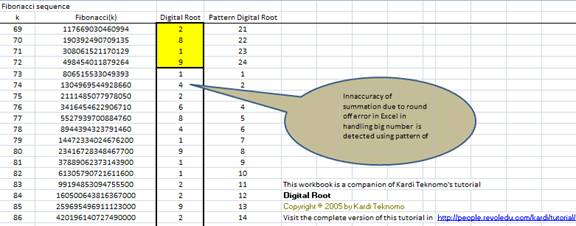
Similar problem may happen in any programming languages aside from MS Excel. It may also happen in any arithmetic operation such as addition, subtraction, multiplication, division and power. Using the pattern of digital root, we can detect the inaccuracy of computation.

< Previous | Next | Contents >

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2005). Digital Root. https:\\people.revoledu.com\kardi\tutorial\DigitSum\