Think of any natural number (positive integer), for example 179. Add all the digits of that number (1 + 7 + 9 = 17). Repeat the addition of the digits until it is only single digit (thus, 17 -> 1 + 7 = 8). The last single digit is called digital root of the number.
Thus, digital root of 179 is 8.
Digital root or sometimes called digit sum of a natural number is a single digit obtained from the iterative summation of the digits in the number. For our base-10 decimal system, the single digit is one of number 1 to 9.
For example, digital root of 123456789012 is 3. Here is the computation:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 1 + 2 = 48
4 + 8 = 12
1 + 2 = 3
Digital root of a natural number can be computed using the following formula
![digitalroot[x]=1+Mod\left [ x-1,9 \right ]](image/digital_root_formula1.gif){kind=small}
Thus, the simplest Macro to obtain digital root is
Function DigitRoot(num As Integer) As Integer
' Return the digital root of 0<num<10^9
DigitRoot = 1 + (num - 1) Mod 9
End Function
Mod is a Modulus function which gives the remainder of a division.
In many programming languages, Mod function has limitation to take argument up to 9 digits number. From number theory, we know that Modulus function has relationship with floor function 
. The backslash is to indicate Mod function. Thus, better way to compute digital root is to use floor function as follow:
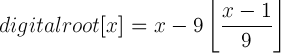
Then, the simple Macro to obtain digital root is
Function DigitalRoot(num as Variant) As Integer
' Return the digital root of num, 0<num<10^28
' Contribution of Robert Sawyer ("r.e.s")
num = CDec(num)
DigitalRoot = x-9*int( (num - 1)/ 9)
End Function
Note however the functions above cannot handle very large number. For example if you use num = 25^25 and use MS Excel (or even Visual Basic), you cannot get the digital root using the formula or simple macro above. [See also the section Power of Digital Root].
If you like iterative programming of digital root of large number, you should check the function below. Optionally, this function also gives the additive persistence value, which is the number of times to transform the original number into digital root. The number of digit input is also not limited only up to 9 or 28 digits as the code above but much higher number of digits (note that double floating point in VB can cover only 324 digits). The idea is to put the inputNum as a sequence of string rather than a number.
Function DigitalRoot(inputNum As Variant, Optional AdditivePersistence As Integer) As Integer
'####################################################
' This function return digital root using iteration
' copyright (c) 2005 by Kardi Teknomo
' see more tutorial in http://people.revoledu.com/kardi/
' inputNum := write the number as a string to get correct result
' additivePersistence= number of transformation from the number until digital root
'####################################################
Dim s As String, sum As Long
Dim i As Integer
Dim num As String
' this validation line can be removed for input of a very large number
' otherwise, you are limited to inputNum<10^309
If Not IsNumeric(inputNum) Or inputNum <= 0 Then Exit Function
s = Trim(inputNum)
Do While Len(s) > 1
sum = 0
For i = 1 To Len(s)
sum = sum + Val(Mid(s, i, 1))
Next
AdditivePersistence = AdditivePersistence + 1
s = Trim(Str(sum))
Loop
DigitalRoot = CInt(s)
End Function
The number of transformation from the number until digital root is called additive persistence . For number 179 we have additive persistence of 2 because it requires 2 transformations from 179 -> 17 -> 8. Another example, number 78945 is transformed into 33 (=7+8+9+4+5) and finally transformed into 6 (=3+3). Thus, 78945 -> 33 -> 6 has additive persistence of 2.
Note that the above digital root function has limited up to 309 digits because of VBA function IsNumeric(x). If you are sure that the input value is Numeric, you can remove the validation line and theoretically you can obtain the digital root of any digit number limited only by your computer memory or other factors. In fact, the stress testing in my computer can run the digital root code above only up to 32,759 digits.
Digital root calculator
Below is Digital root calculator, an interactive program to determine the digital root of your input. Test your own input of digital root. Your input must be positive integer number of any digit up to 65,513 digits. The Example button will provide you with a random number of 15 to 16 digits input. You may play around with large number of digits input.
These tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2005). Digital Root. https:\\people.revoledu.com\kardi\tutorial\DigitSum\