Power of Digital Root
The following interaction program determine the power digital root of your input x^y. Your input must be positive integer number of any digit up to 32,759 digits for base x and 28 digits for exponent y.
Let define dr[x] as digital root of x and dp[x, y] as power of digital root of 
. In this case, we call x as base and y as exponent. Then, based on the pattern of power digital root, we can say these properties:
Power of digital root is equal to the power of the digital root of the base:
dr[z] =dp[x, y] = dp[ dr[x], y]
For instance, we know that 225 = 15^2. Then, we can say that the digital root of 225 is equal to power digital root of 15 with exponent 2. In turn, this equal to the power of 6^2=36 and the digital root of 36 is 9. In formula, it becomes
dr[225] = dr[15^2] = dp[15, 2] = dp[ dr[15], 2] = dp[6, 2] = dr[36] = 9
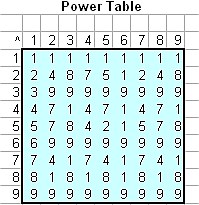
The power of digital root has regular interesting pattern. The base has cycle length 9 and the exponent has cycle length 6. The power of digit root 1 is always 1, thus it has constant pattern whatever the power value is. Digit root 2 has repeating long pattern of 2-4-8-7-5-1. Digit root 3, 6 and 9 has constant pattern of 9 for any value of the exponent except 1. Digit root 4 has repeating pattern of 4-7-1 while digit root 7 has repeating pattern of 7-4-1. Digit root 8 has repeating short pattern of 8-1. [Compare this pattern to Division of Digital Root]
Looking the pattern of digital root below, the pattern of the base is repeating every 9 cycle length and the pattern of the exponent is repeating every 6 cycle length. This pattern can be formulated as the following property:
dr[z] = dp[x, y] = dp[ x+9, y+6] for x=1,2,3,..., y=2,3,4,...
For example, we can add the base with 9 and the exponent with 6 and still get the same digital root
dr[225] = dr[15^2] = dp[15, 2] = dp[15+9, 2+6] = dp[24, 8] = dr[110075314176]=9.
In fact, we can write add only the base value with 9
dp[15, 2] = dp[24, 2] = dp[33, 2] = dp[42, 2] = 9.
Or, we can add only the exponent with 6
dp[15, 2] = dp[15, 8] = dp[15, 14] = dp[15, 20] = 9.
Practically, the pattern of digital root power cannot be produced using simple formula 
because of Mod function in most programming language usually cannot take very large number. One alternative is to use recursive or iterative method (macro) to produce such pattern above. [See the computer code].
The following code and explanation come from the contribution of Robert Sawyer ("r.e.s.") a math hobbyist from the USA.
The power of digital root of x^y can be computed without computing any powers, as follows:
Let dr(x) be the digital root of x, i.e. dr(x) = 1 + (x-1) mod 9. Then
dr(a*b) = dr( dr(a)* dr(b) ), so, if y > 1, then
dr(x^y) = dr( dr(x) * dr(x^(y-1)) ).
Therefore, a function f(x,y) can be defined recursively to compute dr(x^y) without evaluating any powers:
f(x,y)
= dr(x) if y = 1
= dr(dr(x) * f(x, y - 1)) if y > 1.
In Excel Macro, the codes are shown below.
Function RecursiveDigitalPower(x As Integer, y As Integer) As Integer
' return digital root of x^y using the recursive property
' that dr(x^y) = dr( dr(x) * dr(x^(y-1)) ),
' which follows from dr(a*b) = dr( dr(a) * dr(b) )
' as explained by Robert Sawyer.
If y > 1 Then
RecursiveDigitalPower = DigitalRoot(DigitalRoot(x) * RecursiveDigitalPower(x, y - 1))
Else
RecursiveDigitalPower = DigitalRoot(x)
End If
End Function
Another way is to compute the power of digital root iteratively. A power of a number can be written as an iterative function 
for 
and the product of digital root has a nice property of 
. Therefore, we can write the power of digital root dr[z] = dr[x^y] as an iterative function.
Function IterativeDigitalPower (x_, y_)
'return the digital root of x^y (0 < x,y < 10^28)
' contribution of Robert Sawyer (“r.e.s.”)
x = CDec(x_)
y = CDec(y_)
z = CDec(1)
w = DigitalRoot(x)
For i = 1 To y
z = DigitalRoot (z * w)
Next
IterativeDigitalPower = z
End Function
Still another better way to use the nice property of power digital root
dr[z] = dp[x, y] = dp[x+9, y+6]
as explained above. The code below is the best we got so far that it can accommodate the base up to 32,766 digits and exponent up to 28 digits.
Function DigitalPower(x, y)
'computes the digital root of x^y
' return the digital root of x^y (0 < x<10^32766, 0<y < 10^28)
' contribution of Robert Sawyer (“r.e.s.”)
Drx = DigitalRoot(x)
y = CDec(y)
yy = CInt(y - 6 * Int((y - 2) / 6))
z = CDec(1)
For i = 1 To yy
z = DigitalRoot(Z * Drx)
Next
DigitalPower = z
End Function
One easy way to tested the function above is to place the following in a cell
=DigitalPower(CONCATENATE(REPT(9,32765),"8"), CONCATENATE(REPT(9,27),"9"))
which should then display 8 (i.e., the digital root of 8^999...9 with 28 9s). Changing the last digit of x from "8" to "9" should of course change the display to 9. The 999...98 with 32765 9s is chosen because it has a digital root of 8, and 8^n has a digital root that simply alternates between 1 and 8 when n is changed to n+1 or n-1, making it easy to verify that all the digits of y are being processed correctly; i.e., changing the last digit of y from "9" to "8" in the above line should change the display from 8 to 1.
You can download the MS Excel companion of this article here
Historical Note:
I hope this historical note will prevent you from doing the same mistake. In my earlier attempt, I used simple iterative Macro to compute the power of digital root and it was my mistake to deduce that the power of digital roots has complexity pattern as shown below:
On the left side, it is almost regular but getting to the right (higher number of exponent) the pattern is irregular. The boundary between irregular and regular pattern is a curve with two asymptotes in the bases and in the power. The part of irregular pattern is really complex that one cannot predict what will be the next pattern. It is quite amazing that such random pattern can be produced using simple deterministic formula of digital root
The apparent complex pattern above may be generated due to inaccuracy of round off error as suggested by the comment below. If you are interested in complex pattern of digital root, check the next section on digital root of prime number.
Hi Kardi,
I have a general interest in complexity and was intrigued by the
pattern that appeared to be associated with the powers of digital
roots that you published. However, the breakdown of the pattern was
not like the normal onset of chaos.
It was noticeable in the pattern that the solid colour pattern
associated with multiples of nine indicating a digital root of nine
broke down more quickly the larger the multiple. I counted the pixels
and checked the first break down for several multiples of nine on my
calculator. Each time I got a standard representation instead of the
full integer representation. When I reduced the power by one I got
the full integer number and when I multiplied this by nine manually
and calculated the digital root the answer was nine - not the
deviation the pattern indicated.
The maximum number of digits before swapping to standard notation was
14. In .NET and most recent versions of visual basic a long integer
can have up to 19 digits. However, this would not give a sufficient
range of numbers for the pattern you were trying to create. I suspect
therefore that you used double precision numbers which given a much
greater range but unfortunately are only accurate to 14 significant
figures.
You could get around the problem by using the big number class in Java
or writing your own long hand multiplication routines, a language like
Perl or Lisp would probably be ideal although I am sure you could do
it easily enough in VB.
Nigel Phillips
Programme Director BIT
Information Systems & Information Technology
Faculty of Business, Computing and Information Management
London South Bank University
London SE1 0AA
These tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2005). Digital Root. https:\\people.revoledu.com\kardi\tutorial\DigitSum\