|
By Kardi Teknomo, PhD.
<Previous | Next | Contents>
In the previous section, we have learned about one dimensional pattern of digital roots. In this section, we will explore the properties of simple arithmetic of digital roots.
From these operations, we can derive two dimensional pattern of digital root.
Suppose we have two digital roots,  and  , then we would like to know know the results of the arithmetic operation of digital root such as
- Addition
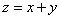
- Subtraction
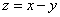
- Multiplication
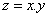
- Division
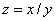
Let us define digital root as a function ![dr[x]=1+\left ( x-1 \right )\setminus 9 = x - 9\frac{x-1}{9}](Image/digital_root_identity_3.gif) , then for all the four operations above, we can say that ![dr\left [ z \right ]= dr\left [ dr\left [ x \right ]\odot dr\left [ y \right ] \right ]](Image/digital_root_group_identity.gif)
Addition 
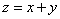
Digital root of a summation is equal to the digital root of the sum of the digital roots of each term: 
For instance, we know that 589 = 214 + 375. Then, we can say that the digital root of 589 is equal to digital root of 214 plus digital root of 375. This gives digital root of 7+6 which is equal to 4. In formula, it becomes
dr[589] = dr [ dr[214] + dr[375] ] = dr[7 + 6] = 4.
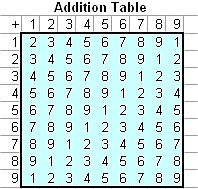
Here is the addition table of digital roots and its pattern.
 
Subtraction 
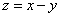
Digital root of a difference is equal to the digital root of the difference of the digital roots of each term: ![dr\left [ z \right ]= dr\left [ dr\left [ x \right ]- dr\left [ y \right ] \right ]](Image/digital_root_subtraction_property.gif)
For instance, we know that 161 = 375-214. Then, we can say that the digital root of 161 is equal to digital root of the difference of digital root of 375 and digital root of 214, that is equal to digital root of 6 – 7 equal to 8. In formula, it becomes
dr[161] = dr[ dr[375] - dr[214] ] = dr[6-7] = 8.
Below is the Subtraction table of digital roots and its pattern
 
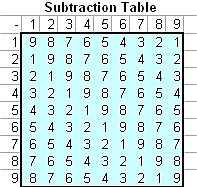
You will see number 9 in the main diagonal and the other digital roots lie in parallel with the diagonal.
Multiplication 
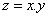
Digital root of a product is the same as the digital root of the multiplication of the digital roots of its factors: 
For instance, we know that 7777 = 77 * 101. Then, the digital root of 7777 is equal to digital root of 5 multiply by digital root of 2, that is the digital root of 10, which is equal to 1. In formula, it becomes
dr[7777] = dr[ dr[77] . dr[101] ] = dr[5.2] = dr[10] = 1.
Below is the Multiplication table of digital roots and its pattern
 
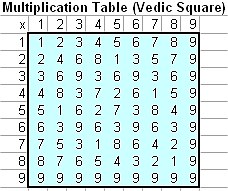
Multiplication table produces many beautiful pattern and properties that worth to put into separate section to describe about it. More about multiplication table, see Vedic Square
Division 
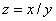
Digital root of a division is equal to the digital root of the difference of the digital roots of each term: ![dr\left [ z \right ]= dr\left[ \frac{dr\left [ x \right ]}{dr\left [ y \right ]} \right ]](Image/digital_root_division_property.gif)
For instance, we know that 31 = 3751/121. Then, we can say that the digital root of 31 is equal to digital root of the division of digital root of 3751 and digital root of 121, that is equal to digital root of 7/4 equal to 4. In formula, it becomes
![dr\left [ 31 \right ]= dr\left[ \frac{dr\left [ 3751 \right ]}{dr\left [ 121 \right ]} \right ] = dr\left[ \frac{dr\left [ 7 \right ]}{dr\left [ 4 \right ]} \right ]=dr\left[\frac{7}{4}\right ]=4](Image/digital_root_division_example.gif)
ee the division table below to obtain the digital root of division
 
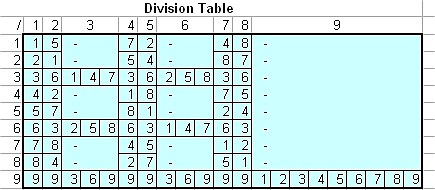
Digital root 3, 6 and 9 are special. Not all numbers can be divided by these three numbers. If the division is allowed, it will produce multiple roots.
Notice that 3, 6 and 9 has no root or multiple roots. For example, 1/3 has no root (undefined, similar to a number divided by zero in decimal system) but 6/3 has multiple roots of 2, 5 and 8. Digital root 9 has no root unless the denominator is also 9 which produce 9 multiple roots of 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Factors
Suppose  ,  and  are digital roots and we have equation  then we have solution  ,
- no solution (no root) if
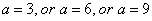 and 
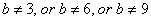
- multiple solutions (multiple roots) if
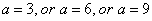 and 
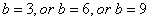
- Single solution (single root) if otherwise
Digital Root Identity
In multiplication and division operations, digital root 1 serves as identity because  and  . In addition or subtraction operations, digital root 9 serves as identity because  and  . In other words, digital root 9 behaves similar to zero in decimal number system.
<Previous | Next | Contents>
Download the MS Excel companion of this tutorial here
These tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2005). Digital Root. http:\\people.revoledu.com\kardi\tutorial\DigitSum\
|
