Vedic Square

By Kardi Teknomo, PhD.

< Previous | Next | Contents >

In the previous section, Vedic square was introduced as multiplication table of digital roots. Vedic square has very rich patterns that worth to explore further about its properties.

Vedic square is a symmetric matrix , that is

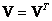
Quadratic pattern is lies in the diagonal of Vedic square: 1497-7941-9

Let us use basic Vedic Square as our matrix and the element of the matrix as

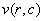
General Vedic square can have any size bigger than 9 by 9. We can then derive several important basic properties for general Vedic square of any size

Top left boundary: . This is to say that the top and left digit sums are equal to its placement.

Bottom Right boundary: . Every multiple of 9, the Vedic square will produce 9

Sum of columns in Vedic square: . For example, second column plus seventh column will always produce the ninth column; third column plus fifth column will produce 8 th column.

Sum of rows in Vedic square: . For example, second row plus seventh row will always produce the ninth row; third row plus fifth row will produce 8 th row.

Cyclical property: .

Many 2 dimensional patterns can be generated using Vedic square, including many Islamic Arts (Jones, 1998). By putting some color to the numbers, we can make many patterns. Below is some example of a few patterns. You can download the MS Excel companion of this article here to try your own pattern.

Tips: Making Vedic Square using Matlab

The function below is useful to obtain Vedic Square using Matlab

function V=Vedic(n, color) 

    if nargin<1 | n<9, n=9; end     % if no input or input less than 9, set n as 9 

    if nargin<2, color='prism'; end % if no input color set color as prism 

    A=[1:n];                        % this is to make n by n Vedic square 

    K=ones(n, n); 

    V=K+mod((A'*A-K),9);            % this is the Vedic square 

    imagesc(V);                     % show Vedic square as image 

    colormap(color);                % change color of image. 
                                    % Try many different color maps 
                                    % such as 'colorcube', 'flag', 'hsv(30)',
                                    % 'jet', 'summer', 'hot', 'prism', etc. 

    axis off;                       % remove the axis label 

Run this code using

>> Vedic(81, 'hot')

In the next section, you will learn about the grouping or cluster of digital root pattern based on multiplication and division tables.

< Previous | Next | Contents >

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2005). Digital Root. https:\\people.revoledu.com\kardi\tutorial\DigitSum\