Fractal in Excel: Sierpinski Gasket

by Kardi Teknomo

Share this: Google+

Sierpinski Gasket using Excel

We are going to make a fractal shape of Sierpinski gasket or sierpiski sieve as shown in the figure below using MS Excel. You do NOT need to make any macro or program; all you need is only simple formula of addition and mod. How can it be? Follow step-by-step procedure below and I will give you the explanation.

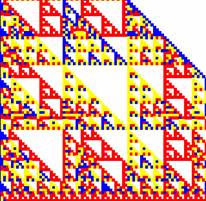Mod 10 Mod 9

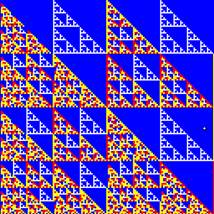Mod 8 mod 22

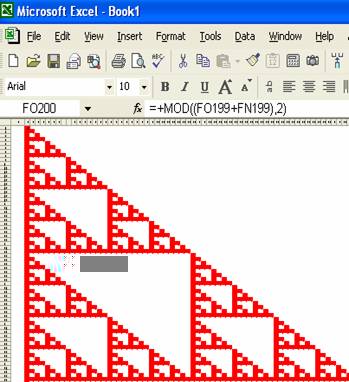
Sierpinski gasket is described by Pickover (1993) using Pascal triangle Mod 2. It is one type of fractal drawing as introduced by Mandelbrot (1982). If you do not know what Pascal triangle is, here is the explanation. Pascal triangle is formed when put binomial coefficient into a table. Binomial coefficient or often-called Combination has formula

Notation is called factorial, symbolize a multiplication of natural number from 1 to , that is . For example, ,

Example of Combination or Binomial coefficient

,

In general,

Extending Binomial coefficients in a table, we will get Pascal triangle

MS Excel has a built-in function =COMBIN(n, r) to generate Combination or binomial coefficient directly. However, we are not going to use this function because MS Excel will have severe round-off error when we perform remainder division or MOD, especially when n and r are large. Instead, we will use simple addition formula to overcome the round-off error. You may notice that in the table of Pascal triangle above, the value of a cell in the Pascal triangle can be computed as a summation of two cells in the row above it: the cell in the same column and the one in the column just to left. We can use this property to generate more stable Pascal triangle.

MOD or modulus is remainder of division. For example, 3 mod 2 is 1 because 3 divided by 2 is equal to 1 with remainder 1. We take only the remainder value, thus 3 mod 2 is 1.

10 mod 5 is 0 because 10/5 = 2 with zero remainder. 12 mod 8 is 4 because 12/8 is equal to 1 with remainder of 4.

Sierpinski gasket is simply a Pascal triangle mod 2. Mod 2 will always produce binary 0 and 1. If we remove the 0 we will see the beauty image of Sierpinski gasket.

Here is the procedure step by step:

1. Open a new sheet. In cell B4, type 1
2. In cell B5, type =MOD((B4+A4),2). This is to compute Pascal triangle mod 2.

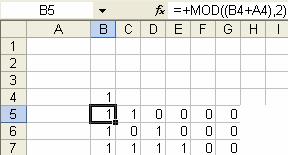
3. Then you can copy cell B5 and paste it to many cells in the right and down by pressing CTRL-C, move down and to the right then CTRL-V

4. Now you can do a little formatting so that it looks nice. While still selecting the cells (if you have click in other cell, you may use SHIFT and you mouse to select the range of cells that contain the formula), click menu Format > Column > AutoFit selection. This will make the column width smaller to fit only binary number.

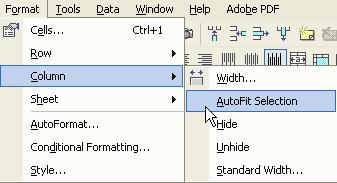
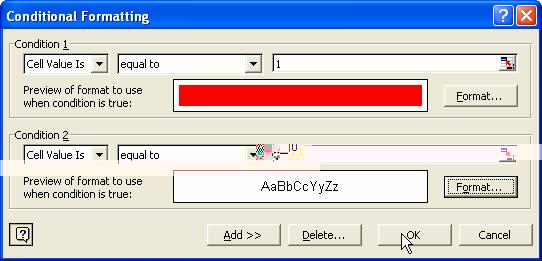
5. While still selecting the range of cells that contain the formulas, click menu Format > Conditional Formatting

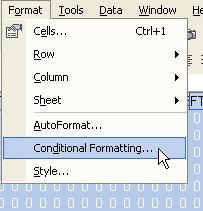
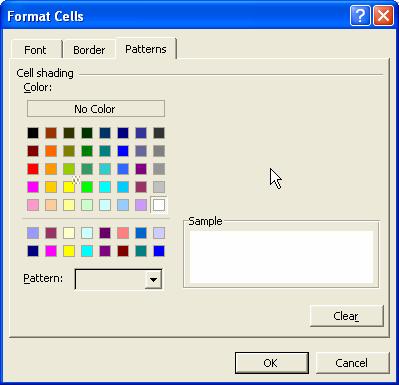
5. a. Put Condition 1: Cell value is equal to 1 and click the format button. In Font tab, set the font color to red, then in the Pattern tab, set the cell shading color also equal to red. Click OK button to the Format cells dialog and click Add >> button in conditional formatting dialog, to add another criteria.

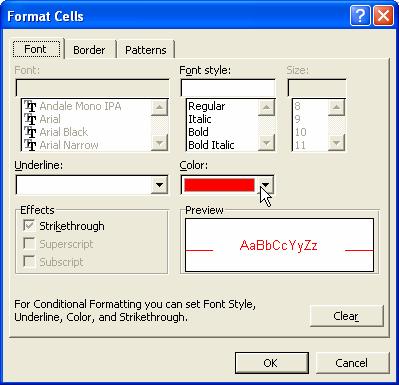
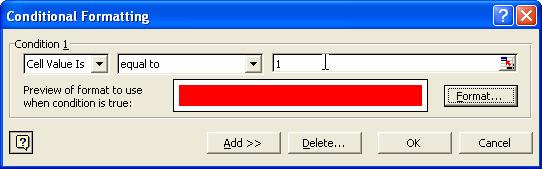
5. b. Put condition 2: Cell value is equal to 0 and click the format button. In Font tab, set the font color to white, then in the Pattern tab, set the cell shading color also equal to white. Click OK button to the Format cells dialog and conditional formatting dialog.

6. To have a better view, you may copy as much as right and down as you can (but it will slow down your computer) and view at 25% zoom.

The Spreadsheet file can be downloaded here

In the workbook, there are several sheets to explain systematic development of Pascal Triangle, Pascal Triangle Mod 2 and Sierpinski gasket. The Sierpinski sheet contains forms that are more general. You may modify the Mod value and color with any integer from 2 and see the beautiful effect of fractal in Pascal triangle.

References:

Mandelbrot, B. (1982) The Fractal Geometry of Nature, Freeman San Francisco

Pickover, Clifford A. (1993) On Computer Graphics and The Aesthetics of Sierpinski Gaskets Formed From Large Pascal's Triangles in: The Visual Mind, Art and Mathematics, Emmer, Michele (Ed), The MIT press, Cambridge .

See also:
MS Excel Tutorial index , Kardi Teknomo's Tutorial , Chaos Ginger Bread man , Fractal from Complex Number

Send your comments, questions and suggestions

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Fractal in Excel: Sierpinski Gasket. https:\\people.revoledu.com\kardi\ tutorial\Excel\Sierpinski.html