Understanding Compound Interest
Suppose you borrow $1000 from a money lender that charge you 1% interest rate per month. You will pay $20 per month to pay your debt. My question is simple: when are you going to pay back your debt? In how many months you will be able to accomplish to pay back your loan?
Let me give you a clue.
Your loan is $1000 and you are paying $20 a month. If there is no interest rate, you should be able to pay back your loan in $1000/$20 = 50 months.
Given the 1% interest rate, can you guess in how many months you will be able to pay back your interest rate?
Is it 51 months? Or, is it 55 months? What is your guess? How to calculate that?
Do not proceed to read unless you have guessed on when are you going to pay back your debt.
(If you are impatient, turn to the next page to know the answer.)
In how many months you will be able to pay $1000 loan at 1% interest rate per month, if you pay $20 a month?
Here are the two formulas to find the answer.
Your loan at time t+1 = Your loan at time t + The interest of your loan at time t � Your monthly payment
The interest of your loan at time t = Interest rate * Your loan at time t
I do not like long words, thus let us simplify the formula above. Suppose we give a notation as follows
L(t) = Your loan at time t
L(t+1) = Your loan at time t+1
k = Interest rate
R(t) = The interest of your loan at time t
P = Your monthly payment
The two formulas above can be written as simple as
L(t+1) = L(t) + R(t) - P
R(t) = k * L(t)
Now we can further simplify the two formulas above into a single formula by substituting the second formula into the first formula.
L(t+1) = L(t) + k * L(t) - P
In the right hand side, you can see two terms contain L(t), which we can combine into our last formula
|
L(t+1) = (1 + k) * L(t) - P |
In word,
|
Your loan at time t+1 = (1 + Interest rate ) * Your loan at time t - Your monthly payment |
In the beginning, at time t=0, you have your loan. Thus, L(0) = $1000.
In the first month, your loan will become
L(t+1) = L(t) + k * L(t) - P
L(1) = L(0) + 1% * L(0) - P
L(1) = $1000 + 1% * $1000 - $20
L(1) = $1000 + $10 - $20
L(1) = $1000 - $10
L(1) = $990
In the second month, your loan will become
L(t+1) = L(t) + k * L(t) - P
L(2) = L(1) + 1% * L(1) - P
L(2) = $990 + 1% * $990 - $20
L(2) = $990 + $9.90 - $20
L(2) = $990 - $10.10
L(2) = $979.90
Computing manually like this would be cumbersome. We need better tool to compute. Let use spreadsheet (like Microsoft Excel, Google Spreadsheet, etc.) to compute.
If you are too lazy to make this spreadsheet on your own, simply donate to Revoledu.Com and contact me, you will get the spreadsheet and the PDF version of this tutorial.
First you type the three inputs
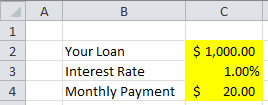
Then you type the following formulas in your spreadsheet
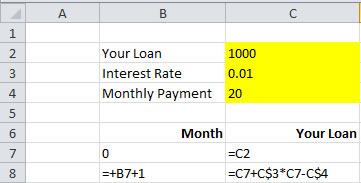
After that you copy cell B8:C8 down until B107:C107.
Next, we do the charting to show when your loan will reach zero.
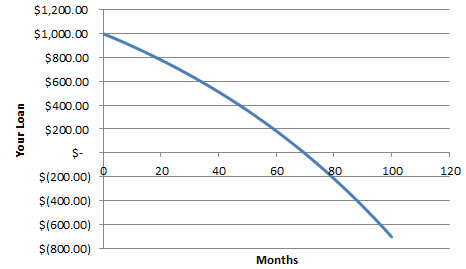
In how many months you will be able to accomplish to pay back your loan?
To see more detail, look at the chart and the spreadsheet on when your loan will cross zero.
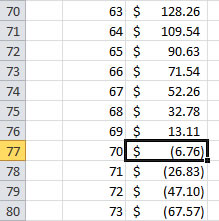
You are right. You will be able to pay your loan in 70 months.
In the next sections, you will learn how such interest rate can make you bankrupt or rich.
Do you like this Tutorial?
Share it with others!
Rate this tutorial or give your comments about this tutorial
