Adaptive Learning with Memory

by Kardi Teknomo

<Contents | Previous | Next >

So far, we have game with simple learning using histogram. The adaptive learning using histogram is simple and powerful. The learning algorithm, however, is only based on total number of user response. It has very short memory of what the user response aside from single previous response. In this section, we will generalize the learning algorithm by adding system memory.

Firstly, we must understand the meaning of system memory. A system with short memory tends to be affected by the most recent behavior of user input. This system has fast or fluctuated response because the output behavior is responding quickly to the change of the input.  System with long memory has sluggish behavior. It does not response as speedily to the change of input behavior.

To add the long memory to our learning system, we remember the characteristics of time-average, which has long-term memory. The recursive formula to compute the time-average is given by:

                                       (A)

Notation  is the time-average of measurement data . When the time  is a natural number 1, 2, 3, 4 …, the graphs of the coefficients are plotted below:

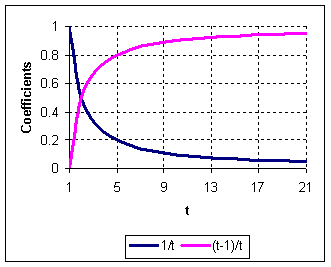
Let us give a new notation  then  and the equation (A) can be written as

                                                 (B)

In the time-average formulation, the value of  is dynamically changing over time. Suppose we fix the value of  as a real number between zero and one inclusive ( ) to represent the learning rate, and replacing the measurement value as probability distribution, we obtain learning probability distribution. In the previous example, we have acquired Probability distribution of failure . This failure probability will serve as input to our learning probability distribution. Adjusting the notation of the equation (B) for probability distribution, we get what is called learning formula (C) with single parameter .

                                  (4)

The range of parameter  is  to produce correct result. Outside this range, the probability may be bigger than one or negative. When the parameter is near to one, the updating of probability is small. Closer the value of  to zero, will produce change that is more sensitive. When . The update of learning probability distribution is only depending on the number of correct and wrong answers (as in the previous example). It has only short memory and do not have depending on the timing when it was answered. When , the learning distribution is updated not only based on the histogram of correct or wrong answers but also based on the timing to answer it correctly. If = 1, the learning probability value never change and whatever user input, the computer will not learn anything.

We can view the parameter   as a learning rate or learning sensitivity value. Sensitive value will make fluctuation change in the learning probability. For example, single wrong answer will change the probability from 25% to 55% or single correct answer may change from 25% to 10%. Less sensitive value (i.e. learning rate near to 1.0) represents the program that learn very slow. For example, to change the learning probability from 20% to 21% demand the user to answer correctly many times.

Another view of the parameter  is as the rate to reach stability. If the equilibrium of the probability distribution exists, (i.e. user has constant learning distribution), with sensitive parameter , the updating probability can reach the equilibrium faster than the insensitive parameter.  Closer the parameter is to one, the updating of probability is will be slower to reach the equilibrium.

The next section we will discuss about the numerical application of the learning formula.

<Contents | Previous | Next >

These tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Learning Algorithm Tutorials. http:\\people.revoledu.com\kardi\ tutorial\Learning\

Send your comments, questions and suggestion to author of this tutorial