<
Previous
|
Next
|
Contents
>
Behavior of Learning Formula
To understand the behavior of the
learning formula
, we continue our previous numerical example
. Table below show again the user responses together with the failure probability and learning probability at
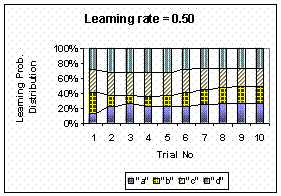
![]() = 0.50.
= 0.50.
Initially, the learning probability distribution is set as uniform distribution with equal probability of for each character. The learning distribution was then updated using learning formula. Based on the learning distribution, we can design the program response so that the characters that have large learning distribution value will be asked more frequently. In the very long trials, if the user has known all the syllables, the learning distribution should approach uniform distribution again.
User response
|
trial no |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a |
Wrong |
Right |
Wrong |
Right |
|||||||
|
b |
Right |
||||||||||
|
c |
Wrong |
Right |
Right |
||||||||
|
d |
Wrong |
Right |
Probability distribution of failure
|
F(a) |
0% |
30% |
31% |
20% |
21% |
24% |
26% |
26% |
27% |
25% |
|
|
F(b) |
33% |
3% |
6% |
15% |
16% |
20% |
23% |
24% |
23% |
24% |
|
|
F(c) |
33% |
33% |
31% |
32% |
32% |
32% |
26% |
23% |
23% |
24% |
|
|
F(d) |
33% |
33% |
33% |
33% |
32% |
24% |
26% |
26% |
26% |
27% |
Learning Probability Distribution (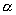 = 0.50)
= 0.50)
|
F(a) |
25% |
13% |
21% |
26% |
23% |
22% |
23% |
24% |
25% |
26% |
26% |
|
F(b) |
25% |
29% |
16% |
11% |
13% |
15% |
17% |
20% |
22% |
23% |
23% |
|
F(c) |
25% |
29% |
31% |
31% |
31% |
31% |
32% |
29% |
26% |
25% |
24% |
|
F(d) |
25% |
29% |
31% |
32% |
33% |
32% |
28% |
27% |
27% |
26% |
27% |
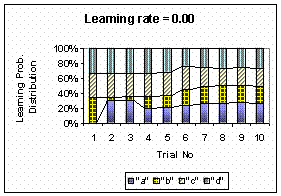
Observe in the table above that the initial probability is very important to determine the behavior of the learning probability distribution. The probability distribution of failure is similar to the learning distribution at zero learning rates. Higher the value of learning rate makes the fluctuation smaller and longer to reach the equilibrium. In this example, the equilibrium values are the initial probabilities (i.e. for each character).
We can view the existing memory in the learning formula dumped the
fluctuation of failure distribution. For example, in trial 2 the failure
probability of character b drops to 3%, while the learning probability
is only drop to 16%. The memory is softening the variability of the
distribution. In trial number 4, the user gives correct answer to character
a and yield learning probability of 23% for character a and only
13% to character b. Notice that character a now has larger learning
probability (will be asked more frequently) than character b because
character a has been questioned 2 times and only one answer correct
while character b has been asked only one time and it yields correct
answer. In trial 7, syllable a, c and d has the same record of
one wrong answer and one correct answer. Their learning probabilities,
however, are not equal. This is happen because the learning rate
![]() is not zero. The learning distribution is updated not only based
on the number of correct or wrong answers but also based on the timing
to answer it correctly or wrongly. The latest correct answers always
get higher learning probability than the old correct answer. At each
trial, the learning probabilities are always relative to each other.
is not zero. The learning distribution is updated not only based
on the number of correct or wrong answers but also based on the timing
to answer it correctly or wrongly. The latest correct answers always
get higher learning probability than the old correct answer. At each
trial, the learning probabilities are always relative to each other.
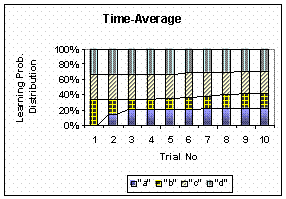
Figure below shows the effect of the learning rate
![]() toward the learning probability distribution. We also include
time-average for comparison. For this 10 number of trials, the time
average is most similar to
toward the learning probability distribution. We also include
time-average for comparison. For this 10 number of trials, the time
average is most similar to
![]() = 0.623 (by minimizing the absolute different. The value of
= 0.623 (by minimizing the absolute different. The value of
![]() is not 0.5 as I first guess it). For longer trials, however,
the learning rate will be different by user responses. Sudden change
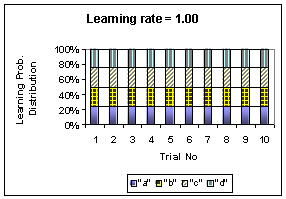
in the distribution is exposed for zero learning rates. For learning
rate
is not 0.5 as I first guess it). For longer trials, however,
the learning rate will be different by user responses. Sudden change
in the distribution is exposed for zero learning rates. For learning
rate
![]() =
1
, the learning probability distribution
is only depending on the initial probability without dynamic update.
=
1
, the learning probability distribution
is only depending on the initial probability without dynamic update.
|
|
|
|
|
|
It worth to mention that although the updating process is independent
among one character to another, the total probability of learning distribution
for all characters are always one. It happens because the total probability
that character
![]() has been successfully answered for all characters
has been successfully answered for all characters
![]() is also one. If this total is not guaranteed, the learning probability
distribution may get incorrect results.
is also one. If this total is not guaranteed, the learning probability
distribution may get incorrect results.
<
Previous
|
Next
|
Contents
>
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Learning Algorithm Tutorials. https:\\people.revoledu.com\kardi\ tutorial\Learning\