Share this:
Google+
< Previous | Next | Contents >
Activation Function of Neural Network
Once a computational neuron receive the inputs from other neurons the neuron aggregates the input values and the synapses weights values into a single value \( s \). After that, they neuron utilize this aggregated value \( s \) into the output value of the neuron \( y \) through activation function. Thus, activation function is the way a neuron utilize the aggregation values from other neurons.
Similar to aggregation function, you can practically define any function to be your activation function.
If we use a threshold function type such as threshold step or binary step or bipolar step function, a neuron cell will be activated only if the value of the sum product is greater than a threshold value. For generality, we can write the output as a non-linear function of the sum product of the weights and the inputs.
| $$ y = f(s) $$ | (5) |
When the inputs of a neuron are binary values, the most common activation function of perceptron is a binary step function as in equation (6) or threshold step function as in equation (7).
| $$ f(s)=\left\{\begin{matrix} 1 \quad if s\geq 0 \\ 0 \quad if s< 0 \end{matrix}\right. $$ | (6) |
For binary step function, when the value of the sum product is positive or zero, the result of the activation function is one. When the value of the sum product is negative, the result of the activation function is zero. For threshold step function, when the value of the sum product is positive, the result of the activation function is one. When the value of the sum product is zero or negative, the result of the activation function is zero.
| $$ f(s)=\left\{\begin{matrix} 1 \quad if s > 0 \\ 0 \quad if s\leq 0 \end{matrix}\right. $$ | (7) |
The graph of binary step function and threshold step function are shown below.
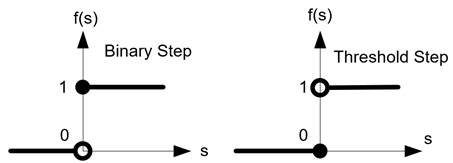
Figure Binary Step and Threshold Step Function
Example
Suppose we the sum product of the synapses weights and the value of the sensory cells of a neuron yields \( s=0.25 \). What would be the output value of the neuron given that the activation function is a binary step function?
Answer:
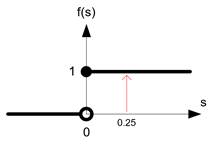
The value of \( s=0.25 \), thus \( s>0 \) (positive) and therefore the output of the neuron is \( y=f(s)=f(0.25)=1 \).
Example
A single layer neural network has two neuron cells and one input cell as shown in the figure below. The value of the weights are \( w_{12}=-2,w_{13}=-0.5 \) and the bias weights are \( w_{02}=1,w_{03}=1.5 \). What are the outputs of the neural network when the input value is 1? What are the output values when the input value is 0? Use threshold step as the activation function.
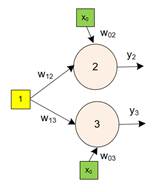
Answer:
First get the sum product and then compute the activation function of each neuron to get the output.
When the input value is 1, we set \( x_{1}=1 \)
$$ s_{2}=w_{02} x_{0} + w_{12} x_{1} = 1\cdot 1+ (-2)\cdot 1 = 1-2 =-1 $$ $$ y_{2}=f(s_{2})=f(-1)=0 $$ $$ s_{3}=w_{03} x_{0} + w_{13} x_{1} = 1.5 \cdot 1 + (-0.5) \cdot 1 =1.5-0.5=1 $$ $$ y_{3}=f(s_{3})=f(1)=1 $$When the input value is 0, we set \( x_{1}=0 \)
$$ s_{2}=w_{02} x_{0} + w_{12} x_{1} = 1 \cdot 1 + (-2)\cdot 0 = 1-0 = 1 $$ $$ y_{2}=f(s_{2})=f(1)=1 $$ $$ s_{3}=w_{03} x_{0} + w_{13} x_{1} = 1.5 \cdot 1 + (-0.5) \cdot 0 =1.5-0=1.5 $$ $$ y_{3}=f(s_{3})=f(1.5)=1 $$The following table is summarized the input and output of this neural network.
input |
Output (activation results) |
| $$ x_{1}=1 $$ | $$ y_{2}=0, y_{3}=1 $$ |
| $$ x_{1}=0 $$ | $$ y_{2}=1, y_{3}=1 $$ |
You can see that a neural network is defined by its weights and its network architecture.
When the inputs of a neuron are continuous values between [0, 1] as in probability values the most common activation function is a sigmoid function type. Sigmoid function has shape of an S curve, as you have learned in table 1, it can be logistic, inverse tangent or hyperbolic tangent function.
| $$ f(s)=\frac{1}{1+exp(-\beta s)},\beta >0 $$ | (8) |
The graph of the sigmoid function is similar to S-curve as shown below. The parameter \( \beta \) is often called the temperature of a neuron. The higher the temperature, the more steep the values of the sigmoid function. The lower the temperature, the curve moves gentler as the value of s changes. In practice, we set the temperature parameter by looking at the range value of \( s \). For instance if the range of values of s is between -1 to +1, setting the value of beta to 10 will give smoother S-curve while setting the value of beta to 0.1 or 0.5 will give linear functions with different slope.
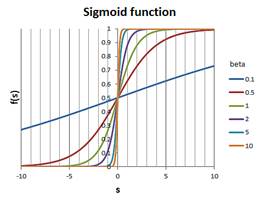
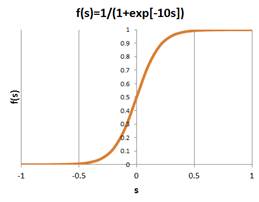
Sigmoid Logistic Function
< Previous | Next | Contents >
Read it off line on any device. Click here to purchase the complete E-book of this tutorial
See Also
:
K means clustering
,
Similarity Measurement
,
Reinforcement Learning (Q-Learning)
,
Discriminant Analysis
,
Kernel Regression
,
Clustering
,
Decision Tree
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2019). Neural NetworkTutorial. https:\\people.revoledu.com\kardi\tutorial\NeuralNetwork\
