Share this:
Google+
< Previous | Next | Contents >
Aggregation Function of Neural Network
Inside a computational neuron, the weights and the inputs to the neurons are interacted and aggregated into a single value. The way we gather the input from the other previous neurons are called aggregation function. There are many aggregation functions but we will focus on the few important ones.
The most important aggregation function is called sum of product. Internally, this neuron will accumulate the sum product of the synapses weights and the input neurons, which includes the bias and the dummy input. This neuron will compute:
| $$ s=w_{0} x_{0} + w_{1} x_{1} + ...+w_{n} x_n = \sum_{i=0}^{n} w_{i} x_{i} $$ | (1) |
If we have more than one computational neurons, the synapses weights are denoted by two subscripts \( ij \). Subscript \( i \) represents the previous neuron and subscript \( j \) represent the current neuron under consideration. The sum of product for current neuron \( j \) is computed as
| $$ s_{j}=w_{0j} x_{0} + w_{1j} x_{1} + ...+w_{nj} x_n = \sum_{i=0}^{n} w_{ij} x_{i} $$ | (2) |
Example
When there are more than one arrows going out of a cell, all of these arrows provide the same value. For example, in the diagram below a sensory cell \( x_{1} \) has two arrows out of the cell. Suppose the value \( x_{1}=1 \). This value would be used as the input to both neuron \( x_{2} \) and \( x_{3} \). Notice we use two subscripts for the synapses weights.
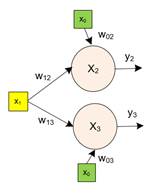
Example
We have a simple neural network with three sensory cells and one neuron. The synapses weight values are given in the diagram below. Suppose the values of the sensory cells are \( x_{1}=0, x_{2}=1, x_{3}=0 \). What is the value of the sum product?
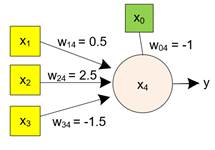
Answer:
$$ s_{4}=w_{04} x_{0} + w_{14} x_{1} + w_{24} x_{2} + w_{34} x_{3} = (-1)\cdot 1+ 0\cdot0.5+1\cdot2.5+0\cdot(-1.5) $$ $$ = -1+0+2.5+0=1.5 $$Note in the diagram above, the two operations inside the neuron are not shown to make the diagram simpler. The number inside neuron represents the bias input value. You have to remember that the operation of sum product and the activation function are always there inside a neuron cell.
Purchase this tutorial to see other aggregation functions
< Previous | Next | Contents >
Read it off line on any device. Click here to purchase the complete E-book of this tutorial
See Also
:
K means clustering
,
Similarity Measurement
,
Reinforcement Learning (Q-Learning)
,
Discriminant Analysis
,
Kernel Regression
,
Clustering
,
Decision Tree
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2019). Neural NetworkTutorial. https:\\people.revoledu.com\kardi\tutorial\NeuralNetwork\

