Neuron Model

By Kardi Teknomo, PhD .

NN

Share this: Google+
< Previous | Next | Contents >

Neuron Model

In this chapter, we will start with the simplest neuron network which consists of only one or many sensory cells and one or many output-neuron cells. There is no hidden-neuron cell.

In 1940’s, McCulloch and Pit [3] proposed a model of simple neuron and Frank Rosenblatt [4] in 1950’s call it perceptron. Perceptron is able to perform many Boolean functions. McCulloch and Pit Neural network has only one neuron while Perceptron may have many neurons. Thus, the perceptron is only handling Boolean values. The perceptron only accept binary inputs and produces only binary outputs.

Later development of neural network includes any normalized input and normalized output values. The normalization goes either from 0 to 1 or from -1 to +1. If the values are not within the range, you need to normalize the values to make them within 0 to 1 or from -1 to +1. When the value of normalization change from binary {0, 1} into bipolar {-1, +1}, the Perceptron model is called ADALINE (see Chapter 8. Single Layer Bipolar Neural Network which discuss about how to solve ADALINE as Excel Solution).

We will use letter \(x\) to symbolize a neuron cell. It is also used to represent the activation results as well as the input value of both sensory cells and dummy cells, such as \( (x_{0},x_{1},...,x_{n}) \). The subscript numbers represent the cell identity number. Let \( n \)  be the number of cells in the neural network, \( n_{input} \) be the number of sensory cells and \( n_{output} \)  is the number of output cells. Since in a single layer neural network model we have only sensory cells and output cells, we have

$$ n = n_{input} + n_{output} $$

Other neuron cells in a neural network that are not part of input neurons and output neurons are called hidden neurons. Let \( n_{hidden} \)  be the number of hidden neurons. In multi-layer neural network model, the number of total neurons is

$$ n = n_{input} + n_{hidden} + n_{output} $$

The term computational neurons are used to represent neuron cells in the hidden neurons and output neurons. Input neurons (including dummy cells and sensory cells) do not do any computation. They simply pass values.

Example

The figure below shows an example of a diagram of a single neuron (name \( x_{3} \)). This output-neuron cell receives two sensory inputs cells (called \( x_{1} \) and \( x_{2} \) ). The output-neuron cell also receives dummy input cell called \( x_{0} \). The activation result as output of the neuron cell is denoted by \( y \) and in the diagram it is symbolized by an output arrow out of the circle. Note that in the example of figure below activation result \( y=x_{3} \).

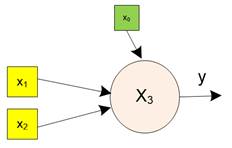
Neuron Model

A neural network can be used to represent either a mathematical function or a mathematical relationship. Do you know the difference between a function and a relationship? A mathematical function may have many inputs and produces only single output. A mathematical relationship may have many inputs and produces many outputs.

A single neuron can receive many inputs and produces a single output. Thus, a single neuron is a mathematical function. The inputs of a neuron would come from three possible sources:

  1. Other neuron cells, or
  2. Sensory cells, or 
  3. Dummy cells.

Now let us go slightly deeper into a neuron cell. Inside a neuron cell (symbolized by a circle), there are usually two operations inside a neuron.

  1. Aggregation function. Most aggregation function is just the summation of the products between weights and the inputs.  This is symbolized by a Greek letter capital sigma \( \Sigma \) .
  2. Activation function denoted by \( f(s) \). There are many activations you can use.

A neuron cell receives input from sensory cells or other neuron cells. These input values from other cells are multiplied by the weight value of the synapsis. Suppose we have a single neuron cell with \( n \) input cells, as illustrated in the diagram below. To remind you of the two operations of aggregation and activity inside a neuron, the symbols of \( \Sigma \) and \( f(s) \) are drawn inside the neuron.

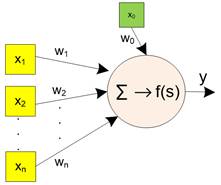
Neuron Model

A Neuron Diagram

< Previous | Next | Contents >

Read it off line on any device. Click here to purchase the complete E-book of this tutorial

See Also :
K means clustering , Similarity Measurement , Reinforcement Learning (Q-Learning) , Discriminant Analysis , Kernel Regression , Clustering , Decision Tree

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2019). Neural NetworkTutorial. https:\\people.revoledu.com\kardi\tutorial\NeuralNetwork\