Euler Method to Solve ODE

< Previous | Next | Contents >

Euler Method (Runge Kutta-1)

Euler method to integrate ordinary differential equation is sometimes also called Runge-Kutta order 1 (RK1) or Euler-Cauchy method.

Suppose we have ODE then

Formula :

Error term : , correct up to the first order term of the Taylor series expansion is

Here is how the Euler method formula is obtained. When we want to find approximation formula that relates and for a very small step , we can use Taylor series expansion of

The big O-notation is the lowest order error term that the Taylor expansion differs from the Euler Method. At each step, the error is relatively big , thus we need very small step size to gain reasonable accuracy. Taking only the first two term of the Taylor expansion, and replace the derivative , we get the Euler method formula (I emphasize that y is a function of x)

Notice that the second term of the right hand side [ ] represents the slope at the beginning of the interval as illustrated in the figure below

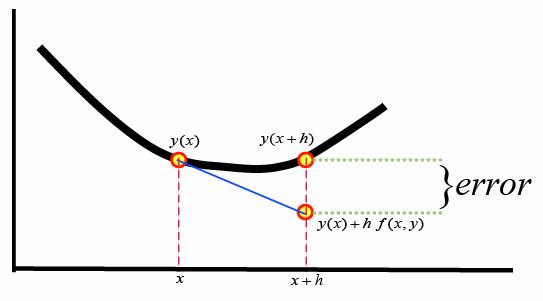
The computation is using spreadsheet that can be downloaded here

Example:

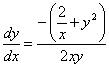, set , with initial condition . The few first results and the graph of solution are also given below.

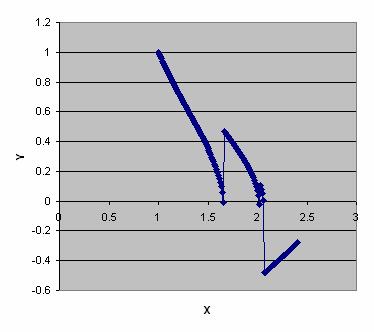
Note that after , the solution is not correct. See Comparison .

< Previous | Next | Contents >

See also: Numerical Excel tutorial , Dynamical System tutorial , Kardi Teknomo's Tutorial

Rate this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Solving Ordinary Differential Equation (ODE). https:\\people.revoledu.com\kardi\tutorial\ODE\