<
Previous
|
Next
|
Contents
>
Quadratic Equation: Optimization without Calculus
In this section, I will show an illustrative example on simple optimization problem (to maximize some objective) and its solution using quadratic function.
Example
Suppose a farmer has a large piece of land and he wants to make a rectangular fence for his animals but he has no money to buy more wood for the fence. Therefore, the total length of the fence is fixed to be
meters. What should the width and length of the rectangle such that the area is maximized?
Solution:
Suppose the width is denoted by
and the length is denoted by
. The perimeter of the rectangle is
and the area of rectangle is
. From the perimeter equation, we can write
and inputting this into the area of rectangle, we obtain
.
This is a quadratic function in the form of
where
,
with parameters
,
and
.
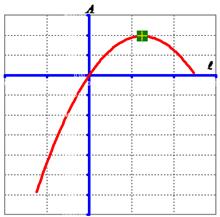
We will use the characteristic of quadratic function to solve this optimization problem. Since the quadratic parameter
is negative, we have sad parabola with maximum extreme point at coordinate
where
is the discriminant. Inputting the values of parameters into the extreme point coordinate, we have
The area of rectangle is maximized at
square meter.
The length of the rectangle is
meter
The width is computed as
meter
Thus, the area of the fenced land is maximized if the boundary is a square with side of 62.5 meter.
Note: Knowing that square shape yield largest area when the perimeter is bounded by the amount of wood he has (
meters), now the farmer asks if he makes the region as circle, will he get larger area or smaller area. The perimeter of circle is
and area of a circle is
. Inputting
into the equation of area of circle yields
square meter, which is actually larger than a square with the same perimeter.
Notice that we do not use any derivative or calculus to solve the optimization problems above.
Go to the next section to find out more resources on quadratic function, equation and formula
<
Previous
|
Next
|
Contents
>
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Quadratic Function Tutorial . http://people.revoledu.com/kardi/tutorial/quadratic/