<
Previous
|
Next
|
Contents
>
Quadratic Parameters
In the
previous section
, we were given quadratic function with known parameters and we must find the root of the quadratic equation where the quadratic function will cross with horizontal axis. In this section, we face different problem where the parameters of the quadratic function are not known. Given arbitrary 3 points on
plane where the
values of those points are distinct, we would like to find the parameters of the quadratic function.
Spreadsheet companion of this tutorial can be downloaded here
.
Pollard (1977)
showed using method of divided differences, we can find the quadratic equation through three distinct points (the
values of those points must be different from each other). Suppose the three distinct points name are
,
and
. We can compute the quadratic function as
Where
,
And
,
,
In the same notation of quadratic function
, we have
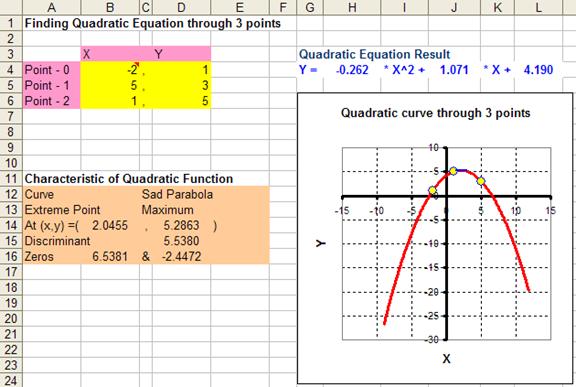
To show above formulation in action, I have implement the above formulation in MS Excel file that can be downloaded here. You can play around with this companion files by modifying the example at yellow cells that represent the coordinate of the three points. Some characteristics of quadratic equations such as extreme points, discriminant and zeros are also computed.
In the next section, you will learn about example of quadratic function application.
<
Previous
|
Next
|
Contents
>
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Quadratic Function Tutorial .
http://people.revoledu.com/kardi/tutorial/quadratic/