<
Previous
|
Next
|
Contents
>
Quadratic Equation
In this section of quadratic function, you will learn about quadratic equation, discriminant, and solving the equation through quadratic formula and modified quadratic formula that is better numerically.
Quadratic equation
is happened to be a special condition of quadratic function
when the parabola curve intersects with the horizontal axis (
). In this case, we can three possibilities:
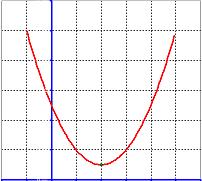
- The quadratic function does not intersect horizontal axis
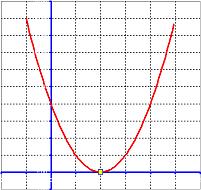
- The quadratic function intersect horizontal axis at single point
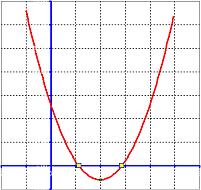
- The quadratic function intersect horizontal axis at two points
|
|
|
|
|
No intersection,
|
Single intersection,
|
Two intersections,
|
The point of intersection between the function and horizontal axis is called the
zeros
of the function, or the
root
of the quadratic equation, because inputting the
values into the quadratic function will make the function value to be zero.
Discriminant
Discriminant
is an index to indicate whether the quadratic function has no intersection (
), intersect as single point (
) or intersect at multiple roots (
) with the horizontal axis. Discriminant of quadratic equation
is computed through its parameters:
When the discriminant is non-negative, given a quadratic equation
, our problem is to solve the equation to find the value of
that satisfied the equation. Solving quadratic equation is actually a process of finding the roots (or the zeros) of the equation.
As this is a well-known problem, the roots of quadratic equation (for multiple roots) are given by quadratic formula:
and
The version, which contains all three parameters of quadratic equation, is sometimes called ABC formula
The roots of quadratic equation are always multiple roots (two roots) except when the discriminant is zero.
For example :
Quadratic equation
contains parameter
,
and
. The discriminant is
. Since the discriminant is negative, we conclude that the equation has no real root (no intersection between the function with horizontal axis). However, the roots exist. The roots are multiple roots in complex number, given by the quadratic formula above
In his interesting paper,
Baker (1998)
pointed out that for quadratic equation
(notice that parameter
), we can get
and
, therefore the quadratic formula above can be written as two terms
The first term (
) is mean or center of mass of the two roots and the second term
(
) is half of the absolute difference of the two roots.
In case of a single (distinct) root, the discriminant is zero, thus lead to
Example
Quadratic equation
has parameters
and
. The discriminant is zero because
. Thus, the root of the quadratic equation is only one, that is
. To check the correctness, we input the root value into the equation to get
which is correct.
Another version of quadratic formula is given as
Press et al (1986)
pointed out that when the value of parameter
and
are both very small, using quadratic formulas above, the root of discriminant will be inaccurate numerically because
and
might cancel each other. They proposed formula that is more robust in term of numerical accuracy
and
Example
Suppose we have a quadratic equation
. We can divide two sides of the equation with 2 to get the equivalent equation of
. Note that now the quadratic parameter is one (
). The other parameters are
and
. The discriminant is
that is positive. Thus, the quadratic equation has multiple roots
Using Press et al modified Quadratic formula we get the same answers
Observe that
and
So far, we have covered only a given quadratic function. In the next section , you will learn how to get the quadratic parameters from data points.
<
Previous
|
Next
|
Contents
>
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Quadratic Function Tutorial .
http://people.revoledu.com/kardi/tutorial/quadratic/