Nominal Distance
In many cases, we cannot measure variable in quantitative way, but it is possible to measure in term of category. A nominal or categorical variable is used when number is only a symbol to represent something. For example, the fruits I like are
1 = Apple,
2 = Banana and
3 = Orange.
Gender is a nominal variable with value of
1 = male and
2 = female.
One main characteristics of nominal or categorical variable is consistent labeling . Order is not important in nominal variable as long as it is consistent. As extreme example, we can change the label of the fruit I like above into
-1 = Orange.
0 = Apple,
+1 = Banana
Gender labeling can be change as
5 = Female,
25 = Male
As long as you consistently remember your own label and use it according to your own label definition, they are valid labels for nominal variable. Of course, you will label them as simple as possible rather than using the extreme labeling.
To calculate distance between two objects represented by nominal variables, we need to consider the number of category in each variable. If the number of category is only two, we can use distance for binary variables such as simple matching, Jaccard's or Hamming distance. If the number of category is more than two, we need to transform these categories into a set of dummies variables that has binary value. There are two methods to transform a categorical nominal variable (with number of category more than 2) into dummy variables:
Method 1: Assign each value of category as a binary dummy variable
Method 2: Assign each value of category into several binary dummy variables
The two methods produce different distances. In both methods, we should avoid preference to the higher number of categories. The distance is computed based on the original variables. Dummy variables that represent values of one original variable must be calculated first before combining this with other variables. The distance between two objects is the ratio of number of unmatched and total dummy variables. If
= number of variables that positive for the
th objects and negative for the
th object and
= number of variables that negative for the
th objects and positive for the
th object, we have
Method 1: Assign each value of category as a binary dummy variable
We assign each value of Mode as a binary dummy variable. The distance between two objects is the ratio of number of unmatched and total dummy variables.
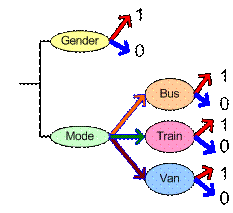
For example, we have two variables: Gender and Mode. Gender has two values: 0 = male and 1 = female. Mode has three choices of public transport mode to go to school: Bus, Train and Van. Suppose we have three subjects: Alex (Male) uses bus, Brian (Male) uses Van and Cherry (Female) use Bus.
We assign each value of Mode as a binary dummy variable. Let set the first coordinate as Gender, while the second coordinate as Mode (Bus, Train, Van). We have
Alex = (0, (1, 0, 0))
Brian = (0, (0, 0, 1))
Cherry = (1, (1, 0, 0))
To compute the distance between object, we need to calculate it for each original variable.
Suppose we use Hamming distance (= length of different digits).
Distance (Alex, Brian) is (0, 2) , overall distance for the two variables is 0+2 = 2
Distance (Alex, Cherry) is (1, 0) , overall distance for the two variables is 1+0 = 1
Distance (Brian, Cherry) is (1, 2) , overall distance for the two variables is 1+2 = 3
The distance between two objects is the ratio of number of unmatched and total dummy variables.
Distance (Alex, Brian) is (0, 2/3), average distance for the two variables is (0+2/3)/2 = 1/3
Distance (Alex, Cherry) is (1, 0) , average distance for the two variables is (1+0)/2 = 1/2
Distance (Brian, Cherry) is (1, 2/3) , average distance for the two variables is (1+2/3)/2 = 5/6
Method 2: Assign each value of category into several binary dummy variables
If the number of categories is
, then we can assign each value of the category into
number of dummy variables with binary value. The number of dummy variables must satisfy condition of
, thus it can be computed as
where
is ceiling symbol.
Ceiling is round up integer away from zero.
For instance, mode of public transportation to school is Bus, Train and Van. We have 3 category, and we need 2 dummy variables because
.
|
Representation |
Bus |
Train |
Van |
|
DV1 |
1 |
1 |
0 |
|
DV2 |
1 |
0 |
1 |
When dummy variable DV1 is 1 and DV2 is 1, it is a bus. When dummy variable DV1 is 1 and DV2 is 0, it is a train and if dummy variable DV1 is 0 and DV2 is 1, it is a van. The assignment to dummy variable is somewhat arbitrary but consistent.
For example, we have two variables: Gender and Mode. Gender has two values: 0 = male and 1 = female. Mode has three choices of public transport mode to go to school: Bus, Train and Van. Suppose we have three subjects: Alex (Male) uses bus, Brian (Male) uses Van and Cherry (Female) use Bus.
We assign each value of Mode into two binary dummy variables. Let set the first coordinate as Gender, while the second coordinate as Mode (DV1, DV2). We have
Alex = (0, (1, 1))
Brian = (0, (0, 1))
Cherry = (1, (1, 1))
To compute the distance between object, we need to calculate it for each original variable.
Suppose we use Hamming distance (= length of different digits).
Distance (Alex, Brian) is (0, 1) , overall distance for the two variables is 0+1 = 1
Distance (Alex, Cherry) is (1, 0) , overall distance for the two variables is 1+0 = 1
Distance (Brian, Cherry) is (1, 1) , overall distance for the two variables is 1+1 = 2
The distance between two objects is the ratio of number of unmatched and total dummy variables.
Distance (Alex, Brian) is (0, 1/2) , average distance for the two variables is (0+1/2)/2 = 1/4
Distance (Alex, Cherry) is (1, 0) , average distance for the two variables is (1+0)/2 = 1/2
Distance (Brian, Cherry) is (1, 1/2) , average distance for the two variables is (1+1/2)/2 = 3/4
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity