What is Similarity and Dissimilarity?
Suppose we have four stars objects as shown in the figure below. Which ones of them are similar? Which ones of them are different?
You may say that star A is similar to star C. Star A, B and C has the same size, while star A, C and D has the same color. Size and color are examples of features that can be measure.
Similarity is quite difficult to measure.
Similarity is quantity that reflects the strength of relationship between two objects or two features.
This quantity is usually having range of either -1 to +1 or normalized into 0 to 1. If the similarity between feature
and feature
is denoted by
, we can measure this quantity in several ways depending on the scale of measurement (or data type) that we have.
Distance measures dissimilarity. Dissimilarity measure the discrepancy between the two objects based on several features . Dissimilarity may also be viewed as measure of disorder between two objects. These features can be represented as coordinate of the object in the features space. There are many types of distance and similarity. Each similarity or dissimilarity has its own characteristics.
Distance is a quantitative variable in general will satisfy the following at least the first three conditions below:
-
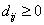distance is always positive or zero
-
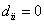distance is zero if and only if it measured to itself
-
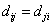distance is symmetry
-
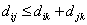distance satisfy triangular inequality
Distance is also called metric if it satisfies all above four conditions. Thus, because of the triangular inequality (condition 4), not all distance are metric, but all metric are distance.
What is the relationship between similarity and dissimilarity?
Let normalized dissimilarity between object
and object
is denoted by
. The relationship between dissimilarity and similarity is given by
(1)
for similarity bounded by 0 and 1. When similarity is one (i.e. exactly similar), the dissimilarity is zero and when the similarity is zero (i.e. very different), the dissimilarity is one.
If the value of similarity has range of -1 to +1, and the dissimilarity is measured with range of 0 and 1, then
(2)
When dissimilarity is one (i.e. very different), the similarity is minus one and when the dissimilarity is zero (i.e. very similar), the similarity is one.
In many cases, measuring dissimilarity (i.e. distance) is easier than measuring similarity. Once we can measure the dissimilarity, we may easily normalize it and convert it to similarity measure.