By Kardi Teknomo, PhD .
<
Previous
|
Next
|
Contents
>
Now suppose you want to make Monte Carlo Simulation of unfair coin. You determine specific probability
to get one of the faces of the coin. If the probability to get zero is
and the probability to get one is
, we can generate a biased coin using the following formula
Formula
Random number
that unformly distributed is generated according to
previous page
. To put this formula in action, I have made a worksheet in MS Excel.
You may download it here
. The explanation of how to use the worksheet is given
below
.
How does the formula work?
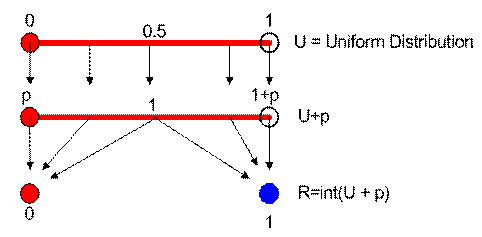
maps the value of
from
into range of
. The
function will round down all values below 1 into 0 and round down all values between 1 and
into 1.
If the value of
is either -1 or 1, then the formula change into
.
In general, if we would like to get the value of
is either
or
, where
with some biased probability
to get
, then
The expected mean is
and the expected variance is
or
How to use the worksheet?
Worksheet companion of this biased coins tutorial can be downloaded here
The sample worksheet uses the two methods above to compute unfair coins. Of course, in many cases you may need to use this more general formula to make 2 integers (not only zero and one, but any numbers
and
)
Every time you press F9, it generates one sampling experiment of Monte Carlo Simulation. If you delete the word "STOP", every time you press F9, you are not only making one sample of numerical simulation; you will add the statistics of the sampling to all samples results. In this way, actually obtain full simple program of Monte Carlo Simulation.
To use the worksheet fully, delete the word "STOP" and press F9 repeatedly. If you don't delete the STOP, the simulation will still work but the result of all experiments are simply copies of the current experiment. Write any letter or number on that Blue cell to reset the counter.
The formula for mean and variance are recursive. You may see more explanation about this recursive formula in my tutorial on Recursive Statistics . If you are still confuse on how to use iteration in MS Excel, please read my tutorial on MS Excel Iteration .
<
Previous
|
Next
|
Contents
>
Give your comments, questions or suggestions for this tutorial
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. Monte Carlo Simulation Tutorial. https:\\people.revoledu.com\kardi\ tutorial\Simulation