What is Brownian Motion?

Share this: Google+
< Previous | Contents | Next >

What is Brownian motion?

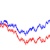
Motivation: Brownian motion is also called Wiener Process is the erratic random movement of microscopic particles in a fluid, as a result of continuous bombardment from molecules of the surrounding medium. It was first observed by botanist Robert Brown in 1827. Norbert Wiener showed the mathematical model of Brownian motion (and therefore Brownian motion is also called Wiener Process). Albert Einstein wrote a paper in 1905 about Brownian motion relation to Avogadro number, Jean Perrin got a Nobel Prize in 1926 for his experimental results in Brownian motion and in 1997 Merton and Scholes a Nobel Prize for the application of Brownian motion in finance, which is called Black–Scholes–Merton model.

Definition: Brownian motion characterized by the following:

At time 0, the initial value is zero
It has stationary non-overlapping independent increment
The increment is Normally distributed
It has almost sure continuous path. There is no jump.

To be more precise, we will use mathematical notation of the definition above. Let $ w_t $ be a Brownian motion (or Wiener Process), then

$w_0 = 0$
Suppose we have $ 0 \leq s_1 < t_1 \leq s_2< t_2 $ , then the increment $w_{t_{1}}-w_{s_{1}} $ and $ w_{t_{2}}-w_{s_{2}} $ are two independent random variables. A stochastic process is called stationary if $ w_t-w_s = w_{t+h} - w_{s+h} $.
Suppose we have $ 0\leq s\leq t $, then the increment $ w_t-w_s \sim N(0,t-s) $ a normal random variable with zero mean and variance $ t-s $.
The path of $ w_t $ over time $ t $ is a continuous function with probability = 1.

Notice that the definition of Brownian motion only include the distribution of the increment but it does not include the distribution of the Brownian motion itself. What is the distribution of Brownian motion? Let us the first and third characteristics of Brownian motion above to define what the distribution of Brownian motion is. We set $ s = 0 $, we have the increment to be $ w_t - w_0 = w_t - 0 = w_t \sim N(0,t) $ . That means Brownian motion is normally distributed with zero mean and variance $ t$. The distribution of $ w_t - w_s, s < t $ would be the same as $ w_{t-s} = w_{t-s} - w_0 \sim N(0,t-s) $. The variance is proportional to the length of interval [s, t]. However, in general $ w_{t-s}\neq w_t - w_s $.

We can also write Brownian motion as

$$ w_t \sim \sqrt{t} N(0,1) = N(0,t) $$

To simulate Brownian motion with one time step, we use uniformly distributed random number to the inverse of cumulative normal distribution to produce $ N(0,1) $.

$$ w_{t+1} = w_t + N(0,1) $$

Brownian motion also has a scaling property such that $ w_{\lambda t}$ has the same distribution as $ \sqrt{\lambda} w_t$.

Note that Brownian motion is only continuous path but not smooth. To get the length of the path, we use integral. However, because the path is not smooth, it is not differentiable. Therefore, we cannot use ordinary integration (i.e. Riemann integration). Fortunately, there is a way to do integration for non-smooth path and that integration is called Ito integration.

< Previous | Contents | Next >