Arithmetic Brownian Motion

Share this: Google+
< Previous | Contents | Next >

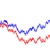
What is Arithmetic Brownian Motion?

A Brownian motion with drift is called arithmetic Brownian motion or ABM. The actual model of ABM is a stochastic differential equation (SDE) of this form

$$ dX_t=m dt+s dw_t $$

This model has two parameters:

1.Drift, $ m $
2.Volatility,$ s\geq 0 $ (sometimes it is also called diffusion coefficient)

The meaning of drift parameter is a trend or growth rate. If the drift is positive, the trend is going up over time. If the drift is negative, the trend is going down. The meaning of volatility is a variation or the spread of distribution. The value of volatility is always positive (or zero) because it is actually related to standard deviation of the distribution.

To simulate the ABM, we need to find the solution of the stochastic differential equation above. The solution can be found by the usual integration to be:

$$ X_t=x_0+mt+sw_t $$

Or,

$$ X_t-x_0=mt+sw_t $$

Notice that ABM contains Brownian motion (or Wiener Process) $ w_t $. This model now has three inputs that is 2 parameters and one initial value:

Drift, $ m $
Volatility,$ s\geq 0 $
Initial value of the ABM, $ x_0 $.

The reason we use symbol $ m $ for the drift parameter and $ s $ for the volatility is because $ X_t $ is normally distributed with mean $ x_0+mt $ and variance $s^2 t $ .

< Previous | Contents | Next >