What is Brownian Motion?

Share this: Google+
< Previous | Contents | Next >

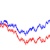
What is Geometric Brownian Motion?

An exponential Brownian motion is also called Geometric Brownian motion, or GBM. This process is suggested by Black, Scholes and Merton. The actual model of GBM is a stochastic differential equation (SDE) of this form

$$ dX_t = \mu X_t dt + \sigma X_t dw_t $$

$$ \frac{dX_t}{X_t} = \mu dt + \sigma dw_t $$

Suppose $X_t $ is price, then this model say that the proportional change in the price in the interval of $ (t,t+dt) $

Similar to AGM SDE, this GBM SDE model also has two parameters:

Drift, $ \mu $
Volatility, $ \sigma \geq 0 $

The meaning of drift parameter is a trend or growth rate. If the drift is positive, the trend is going up over time. If the drift is negative, the trend is going down. The meaning of volatility is a variation or the spread of distribution. The value of volatility is always positive (or zero) because it is actually related to standard deviation of the distribution. Note that the drift parameter of GBM is not the same as the drift parameter of ABM. Similarly, the volatility of GBM is not the same value as the volatility of ABM. In fact, the distribution are not the same.

To simulate the GBM, we need to find the solution of the stochastic differential equation above. The solution can be found by the Ito integration to be:

$$ X_t=x_0 e^{\tilde{\mu t} + \sigma w_t } $$

Where $ \tilde{\mu} = \mu -\frac{1}{2}\sigma^2 $

If we input all, we have

$$ X_t=x_0 e^{(\mu -\frac{1}{2}\sigma^2)t + \sigma w_t} $$

This model can be simplified further by setting $ Y_t=\tilde{\mu}t + \sigma w_t $

Then we have

$$ X_t=x_0 e^{Y_t} $$

If we take natural logarithm on both side, we have a linear model:

$$ \ln\frac{X_t}{x_0}=\tilde{\mu}t+\sigma w_t $$

Notice that GBM also contains Brownian motion (or Wiener Process) $ w_t $. This model now has three inputs that is 2 parameters and one initial value:

Drift, $ \mu $
Volatility,$ \sigma \geq 0 $
Initial value of the GBM, $ x_0 $.

Unlike AGM that is normally distributed, GBM $ X_t $ is log-normally distributed with mean $ x_0e^\tilde{\mu}t $ and variance $ x_{0}^{2} e^{2\tilde{\mu}t} (e^{\sigma^2t}-1) $.

< Previous | Contents | Next >